题目内容
2014年9月初,台湾曝“地沟油”大案,味全、85度C和美心集团等知名企业纷纷中招.内陆某食品企业在政府部门的支持下,进行技术攻关,新上了一种从“食品残渣”中提炼出生物柴油的项目,经测算,该项目处理成本y(元)与月处理量x(吨)之间的函数可以近似的表示为:y=
,且每处理一吨“食品残渣”,可得到能利用的生物柴油价值为200元,若该项目不获利,政府将补贴.
(1)当x∈[200,300)时,判断该项目能否获利?如果获利,求出最大利润;如果不获利,则政府每月至少需要补贴多少元才能使该项目不亏损;
(2)该项目每月处理量为多少吨时,才能使每吨的平均处理成本最低?
|
(1)当x∈[200,300)时,判断该项目能否获利?如果获利,求出最大利润;如果不获利,则政府每月至少需要补贴多少元才能使该项目不亏损;
(2)该项目每月处理量为多少吨时,才能使每吨的平均处理成本最低?
考点:分段函数的应用
专题:函数的性质及应用
分析:(1)先确定该项目获利的函数,再利用配方法确定不会获利,从而可求政府每月至少需要补贴的费用;
(2)确定食品残渣的每吨的平均处理成本函数,分别求出分段函数的最小值,即可求得结论.
(2)确定食品残渣的每吨的平均处理成本函数,分别求出分段函数的最小值,即可求得结论.
解答:
解:(1)当x∈[200,300)时,该项目获利为S,则S=200x-(
x2-200x+80000)=-
(x-400)2,
∴当x∈[200,300)时,S<0,因此,该项目不会获利
当x=300时,S取得最大值-5000,所以政府每月至少需要补贴5000元才能使该项目不亏损;
(2)由题意知,食品残渣的每吨的平均处理成本为
①当x∈[120,144)时,
=
x2-80x+5040,∴当x=120时,
取得最小值240;
②当x∈[144,500)时,
=
x+
-200,
当且仅当
x=
,即x=400时,
≥2
-200,即
取得最小值200
∵200<240
∴每月处理量为400吨时,才能使每吨的平均处理成本最低.
| 1 |
| 2 |
| 1 |
| 2 |
∴当x∈[200,300)时,S<0,因此,该项目不会获利
当x=300时,S取得最大值-5000,所以政府每月至少需要补贴5000元才能使该项目不亏损;
(2)由题意知,食品残渣的每吨的平均处理成本为
| y |
| x |
①当x∈[120,144)时,
| y |
| x |
| 1 |
| 3 |
| y |
| x |
②当x∈[144,500)时,
| y |
| x |
| 1 |
| 2 |
| 80000 |
| x |
当且仅当
| 1 |
| 2 |
| 80000 |
| x |
| y |
| x |
|
| y |
| x |
∵200<240
∴每月处理量为400吨时,才能使每吨的平均处理成本最低.
点评:本题考查函数模型的构建,考查函数的最值,考查利用数学知识解决实际问题,解题的关键是确定函数关系式.

练习册系列答案
相关题目
已知两点A(1,-2),B(-3,4),则以AB为直径的圆的方程为( )
| A、(x+1)2+(y-1)2=13 |
| B、(x-1)2+(y+1)2=13 |
| C、(x+1)2+(y-1)2=52 |
| D、(x-1)2+(y+1)2=52 |
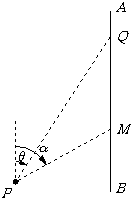 如图,P为某湖中观光岛屿,AB是沿湖岸南北方向道路,Q为停车场,PQ=
如图,P为某湖中观光岛屿,AB是沿湖岸南北方向道路,Q为停车场,PQ=