题目内容
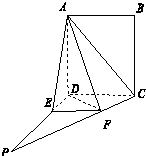如图，四边形ABCD为正方形，PD⊥平面ABCD，PD=AD，AF⊥PC于点F，FE∥CD交PD于点E．（1）证明：CF⊥平面ADF；
（2）若AC∩BD=O，证明FO∥平面AED．
考点：直线与平面垂直的判定,直线与平面平行的判定
专题：空间位置关系与距离
分析：（1）要证CF⊥平面ADF，需要证明CF垂直面ADF内两相交直线，由AF⊥PC于点F，只需证明AD⊥CF
（2）根据已知和（1），只要证明F是CP中点即可．
（2）根据已知和（1），只要证明F是CP中点即可．
解答：
证明：（1）由PD⊥平面ABCD，得PD⊥AD又AD⊥DC，AD∩DC=C根据线面垂直的判定定理，得AD⊥平面PDC
⇒又CF?面PCD，得AD⊥CF，又AF⊥CF，AF∩CF=C根据线面垂直的判定定理，得CF⊥平面ADF
（2）因为AD=PD，由（1）知，F为PC中点．∵ABCD为正方形，AC∩BD=O，∴O是AC中点，连接FO，
则FO是三角形ACP的边AP的中位线，∴FO∥AP，又∵AP?面APD，FO?面APD，根据线面平行的判定定理，
∴FO∥面APD，即FO∥面AED．
⇒又CF?面PCD，得AD⊥CF，又AF⊥CF，AF∩CF=C根据线面垂直的判定定理，得CF⊥平面ADF
（2）因为AD=PD，由（1）知，F为PC中点．∵ABCD为正方形，AC∩BD=O，∴O是AC中点，连接FO，
则FO是三角形ACP的边AP的中位线，∴FO∥AP，又∵AP?面APD，FO?面APD，根据线面平行的判定定理，
∴FO∥面APD，即FO∥面AED．
点评：本题考查了线面垂直于线面平行的判定，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
若关于x的方程
=kx2有四个不同的实数解，则k的取值范围为（ ）
| |x| |
| x+4 |
| A、（0，1） | ||
B、(
| ||
C、(
| ||
| D、（1，+∞） |
登上一个四级的台阶，可以选择的方式共有（ ）种．
| A、3 | B、4 | C、5 | D、8 |
已知两点A（1，-2），B（-3，4），则以AB为直径的圆的方程为（ ）
| A、（x+1）2+（y-1）2=13 |
| B、（x-1）2+（y+1）2=13 |
| C、（x+1）2+（y-1）2=52 |
| D、（x-1）2+（y+1）2=52 |
函数y=loga（x-1）+1（a＞0且a≠1）的图象必经过点（ ）
| A、（0，1） |
| B、（1，0） |
| C、（2，1） |
| D、（0，2） |