题目内容
已知函数f(x)是定义在(-∞,+∞)上的奇函数.当x∈(-∞,0)时,f(x)=1-x-x4.则f(x)={ .
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:坚持求谁设谁的原则,设x>0,则-x<0,将-x代替x代入1-x-x4中,得f(-x)=1+x-x4,利用函数奇偶性即可求得f(x).
解答:
解:设x∈(0,+∞),则-x∈(-∞,0),由x∈(-∞,0)时,f(x)=1-x-x4
得f(-x)=1-(-x)-(-x)4=1+x-x4,又f(x)是奇函数,得f(-x)=-f(x),
故f(x)=-f(-x)=x4-x-1,且f(0)=0,
∴f(x)=
故答案为:f(x)=
得f(-x)=1-(-x)-(-x)4=1+x-x4,又f(x)是奇函数,得f(-x)=-f(x),
故f(x)=-f(-x)=x4-x-1,且f(0)=0,
∴f(x)=
|
故答案为:f(x)=
|
点评:本题开除了利用函数奇偶性求函数解析式的法---代入法,所以基础题,但是容易出错.

练习册系列答案
相关题目
已知向量
=(-2,-6),|
|=
,
•
=-10,则向量
与
的夹角为( )
| a |
| b |
| 10 |
| a |
| b |
| a |
| b |
| A、150° | B、-30° |
| C、-60° | D、120° |
函数y=loga(x-1)+1(a>0且a≠1)的图象必经过点( )
| A、(0,1) |
| B、(1,0) |
| C、(2,1) |
| D、(0,2) |
已知△ABC中,a=3,b=
,∠A=60°,则∠B等于( )
| 3 |
| A、30° |
| B、60° |
| C、30°或150° |
| D、60°或120° |
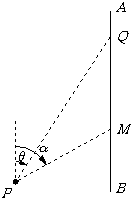 如图,P为某湖中观光岛屿,AB是沿湖岸南北方向道路,Q为停车场,PQ=
如图,P为某湖中观光岛屿,AB是沿湖岸南北方向道路,Q为停车场,PQ=