题目内容
已知向量
=（1，x），
=（-1，x），若2
-
与
垂直，则|
|= ．
| a |
| b |
| a |
| b |
| b |
| b |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：利用向量垂直与数量积的关系、模的计算公式即可得出．
解答：
解：∵向量
=（1，x），
=（-1，x），
∴
•
=-1+x2，|
|=
，
∵2
-
与
垂直，
∴(2
-
)•
=2
•
-
2=0，
∴2（-1+x2）-（1+x2）=0，解得x2=3．
∴|
|=
=2．
故答案为：2．
| a |
| b |
∴
| a |
| b |
| b |
| 1+x2 |
∵2
| a |
| b |
| b |
∴(2
| a |
| b |
| b |
| a |
| b |
| b |
∴2（-1+x2）-（1+x2）=0，解得x2=3．
∴|
| b |
| 1+x2 |
故答案为：2．
点评：本题考查了向量垂直与数量积的关系、模的计算公式，属于基础题．
练习册系列答案
课时训练江苏人民出版社系列答案
黄冈经典趣味课堂系列答案
启东小题作业本系列答案
相关题目
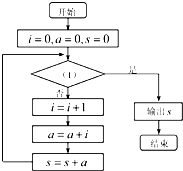在数列{an}中，a1=1，an=an-1+n，n≥2，为计算这个数列前10项的和S，现给出该问题算法的程序框图（如图所示），则图中判断框（1）处合适的语句是
若向量
=（1，1-x），
=（1，1+x），则函数f（x）=
是（ ）
| a |
| b |
| ||||||
| 4-|x-4| |
| A、奇函数 | B、偶函数 |
| C、非奇非偶函数 | D、减函数 |