题目内容
设a∈R,f(x)=
|x-a|
(1)若函数f(x)在[0,+∞)为单调函数,求实数a的取值范围;
(2)设a>0,
(i)证明:函数F(x)=f(x)-
x有3个零点;
(ii)若存在实数t(t>a),当x∈[0,t]时函数f(x)的值域为[0,
],求实数a的取值范围.
| x |
(1)若函数f(x)在[0,+∞)为单调函数,求实数a的取值范围;
(2)设a>0,
(i)证明:函数F(x)=f(x)-
| 1 |
| 2 |
(ii)若存在实数t(t>a),当x∈[0,t]时函数f(x)的值域为[0,
| t |
| 2 |
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值,导数在最大值、最小值问题中的应用
专题:证明题,导数的综合应用
分析:(1)对a讨论,分a≤0,a>0两种,将绝对值去掉,求导数,从而判断单调性;
(2)令F(x)=0则x=0或|x-a|=
,对后一个两边平方,转化为二次方程,判断它有两个不同的正根即可;
(3)考虑函数y1=
(a-x)(0≤x≤a)的极大值点
,从而当x∈[0,t]时,f(x)max=max{f(
),f(t)},分别讨论f(x)max=f(t)和f(x)max=f(
),得到不等式组,解出t的范围,从而得出a的取值范围.
(2)令F(x)=0则x=0或|x-a|=
| 1 |
| 2 |
| x |
(3)考虑函数y1=
| x |
| a |
| 3 |
| a |
| 3 |
| a |
| 3 |
解答:
解:(1)显然x≥0,
当a≤0时,f(x)=
|x-a|=
(x-a),
f'(x)=
x
-
ax-
≥0,
所以f(x)在(0,+∞)上单调递增,符合题意.
当a>0时,f(x)=
,
此时x=a为函数f(x)的极值点,显然不单调.
综上,实数a的取值范围是a≤0;
(2)若a>0,
(i)即证明方程
|x-a|=
x有三个不同的实根,
可化为x=0或|x-a|=
①
①式可化为x2-(2a+
)x+a2=0,
设g(x)=x2-(2a+
)x+a2,
又因为g(0)=a2>0,对称轴x=a+
>0,
且△=a+
>0,
故g(x)=0有两个不同的正根,
即函数F((x)=f(x)-
x有3个零点;
(ii)由(i)知 函数y=f(x)与y=
x有3个交点,
y1=
(a-x)(0≤x≤a)的一个极大值点为x=
,
则当x∈[0,t]时,f(x)max=max{f(
),f(t)},
依题意有:(1)当f(x)max=f(t)时,
则有
即
,
由第二个式子得,a=t-
,代入第一式平方得:
16(t-
)3≤27t2,
即16(
-
)3-27
≤0,
得 16(
)3-24(
)2-15
-2=(
-2)(4
+1)2≤0,
得t≤4,所以a≤3,
又a>0,综上得:0<a≤3.
(2)当f(x)max=f(
)时,则有
即
由①得a3=
t2,由②得:a≥t-
,
所以16(t-
)3≤27t2,同上有0<a≤3,
综上,符合题意的实数a的取值范围是:0<a≤3.
当a≤0时,f(x)=
| x |
| x |
f'(x)=
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
所以f(x)在(0,+∞)上单调递增,符合题意.
当a>0时,f(x)=
|
此时x=a为函数f(x)的极值点,显然不单调.
综上,实数a的取值范围是a≤0;
(2)若a>0,
(i)即证明方程
| x |
| 1 |
| 2 |
可化为x=0或|x-a|=
| 1 |
| 2 |
| x |
①式可化为x2-(2a+
| 1 |
| 4 |
设g(x)=x2-(2a+
| 1 |
| 4 |
又因为g(0)=a2>0,对称轴x=a+
| 1 |
| 8 |
且△=a+
| 1 |
| 16 |
故g(x)=0有两个不同的正根,
即函数F((x)=f(x)-
| 1 |
| 2 |
(ii)由(i)知 函数y=f(x)与y=
| 1 |
| 2 |
y1=
| x |
| a |
| 3 |
则当x∈[0,t]时,f(x)max=max{f(
| a |
| 3 |
依题意有:(1)当f(x)max=f(t)时,
则有
|
|
由第二个式子得,a=t-
| ||
| 2 |
16(t-
| ||
| 2 |
即16(
| t |
| 1 |
| 2 |
| t |
得 16(
| t |
| t |
| t |
| t |
| t |
得t≤4,所以a≤3,
又a>0,综上得:0<a≤3.
(2)当f(x)max=f(
| a |
| 3 |
|
|
由①得a3=
| 27 |
| 16 |
| ||
| 2 |
所以16(t-
| ||
| 2 |
综上,符合题意的实数a的取值范围是:0<a≤3.
点评:本题主要考查导数在函数中的综合应用:求单调性、求极值、求最值,考查分类讨论的思想方法,含参问题的求法,考查运算和推理能力,是一道很好的综合题.

练习册系列答案
相关题目
已知复数方程
=i(i为虚数单位),则复数z的虚部为( )
| 1+i |
| 3i+z |
| A、2 | B、4i | C、-2 | D、-4 |
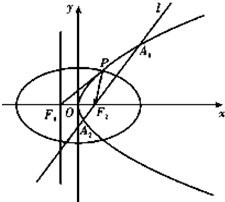 如图,设抛物线
如图,设抛物线 如图,函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|≤
如图,函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|≤