题目内容
点P是双曲线
-
=1右支上一点,F1,F2分别是该双曲线的左,右焦点,点M为线段PF2的中点.若△OMF2的面积为10,则点P到该双曲线的左准线的距离为( )
| x2 |
| 9 |
| y2 |
| 16 |
A、3
| ||||
B、3
| ||||
C、3
| ||||
D、3
|
考点:双曲线的简单性质
专题:计算题
分析:先利用三角形中线性质计算焦点三角形PF1F2的面积,从而得点P的纵坐标,代入双曲线方程即可得点P的横坐标,再利用双曲线标准方程求其左准线方程,进而求得所求距离
解答:
解:∵M为线段PF2的中点,△OMF2的面积为10,∴△OPF2的面积为20,
又∵O为F1F2的中点,∴△PF1F2的面积为40
设P(x,y),则40=
|F1F2|×|y|=
×10×|y|,∴y=±8,代入
-
=1得x=3
∴点P的横坐标为x=3
∵双曲线
-
=1的左准线方程为x=-
=-
∴点P到该双曲线的左准线的距离为|3
-(-
)|=3
+
故选 B
又∵O为F1F2的中点,∴△PF1F2的面积为40
设P(x,y),则40=
| 1 |
| 2 |
| 1 |
| 2 |
| x2 |
| 9 |
| y2 |
| 16 |
| 5 |
∴点P的横坐标为x=3
| 5 |
∵双曲线
| x2 |
| 9 |
| y2 |
| 16 |
| a2 |
| c |
| 9 |
| 5 |
∴点P到该双曲线的左准线的距离为|3
| 5 |
| 9 |
| 5 |
| 5 |
| 9 |
| 5 |
故选 B
点评:本题主要考查了双曲线的标准方程及其几何性质,焦点三角形中的计算问题,求得点P的横坐标是解决本题的关键,属基础题

练习册系列答案
相关题目
已知某个几何体的三视图如右,那么可得这个几何体的体积是( )
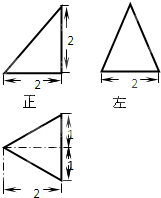

A、
| ||
B、
| ||
C、
| ||
D、
|
已知不等式组
所表示的平面区域为面积等于1的三角形,则实数k的值为( )
|
| A、-1 | ||
B、-
| ||
C、
| ||
| D、1 |
已知实数k满足
>1.则方程x2-kx+1=0的两个根可分别作为( )
| 1 |
| k-2 |
| A、一椭圆和一双曲线的离心率 |
| B、两抛物线的离心率 |
| C、一椭圆和一抛物线的离心率 |
| D、两椭圆的离心率 |