题目内容
已知函数f(x)=
.
(Ⅰ)若函数f(x)在x=0处的切线l0与x=1处的切线l1相互平行,求实数a的值及此时函数f(x)的单调区间;
(Ⅱ)若0<a<4,求证:exf(x)<(a+1+aexlnx)(x2+ax+a).
| x2+ax+a |
| ex |
(Ⅰ)若函数f(x)在x=0处的切线l0与x=1处的切线l1相互平行,求实数a的值及此时函数f(x)的单调区间;
(Ⅱ)若0<a<4,求证:exf(x)<(a+1+aexlnx)(x2+ax+a).
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的单调性,利用导数研究函数的极值
专题:计算题,证明题
分析:(I)先求导函数,然后函数f(x)在x=0处的切线l0与x=1处的切线l1相互平行,则f′(0)=f′(1),求出a的值,最后利用导数符号确定函数的单调性,即可求出函数的单调区间.
(II)原不等式等价于ex
<(a+1+aexlnx)(x2+ax+a),也等价于即
<
+axlnx,
设g(x)=
+axlnx,h(x)=
,利用导数工具研究这两个函数的单调性的最值,可知g(x)≥h(x)恒成立,又因为这两个函数不在同一点取最值,从而得出原不等式成立.
(II)原不等式等价于ex
| x2+ax+a |
| ex |
| x |
| ex |
| a+1 |
| e |
设g(x)=
| a+1 |
| e |
| x |
| ex |
解答:
解:(I)由函数f(x)在x=0处的切线l0与x=1处的切线l1相互平行,
知:f′(0)=f′(1),
而f′(x)=
,∴
=
,解得a=1,
此时f′(x)=
,令f′(x)≥0,得0≤x≤1,
故函数f(x)的单调递减区间是(-∞,0)和(1,+∞),单调递减区间是(0,1);
(II)证明:原不等式等价于ex
<(a+1+aexlnx)(x2+ax+a).
∵0<a<4,∴x2+ax+a>0,原不等式等价于ex<a+1+aexlnx,
即
<
+axlnx,
设g(x)=
+axlnx,h(x)=
,
对于g(x),列表如下:
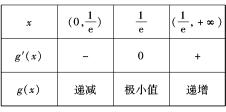
可知,g(x)≥g(
)=
;
对于h(x),列表如下:
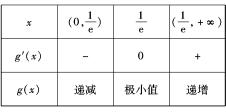
可知,h(x)≤h(1)=
;
综上所述,g(x)≥h(x)恒成立,又因为这两个函数不在同一点取最值,
于是g(x)>h(x)恒成立,
从而 原不等式成立.
知:f′(0)=f′(1),
而f′(x)=
| -x(x+a-2) |
| ex |
| 0×(0+a-2) |
| e0 |
| -(1+a-2) |
| e1 |
此时f′(x)=
| -x(x-1) |
| ex |
故函数f(x)的单调递减区间是(-∞,0)和(1,+∞),单调递减区间是(0,1);
(II)证明:原不等式等价于ex
| x2+ax+a |
| ex |
∵0<a<4,∴x2+ax+a>0,原不等式等价于ex<a+1+aexlnx,
即
| x |
| ex |
| a+1 |
| e |
设g(x)=
| a+1 |
| e |
| x |
| ex |
对于g(x),列表如下:

可知,g(x)≥g(
| 1 |
| e |
| 1 |
| e |
对于h(x),列表如下:

可知,h(x)≤h(1)=
| 1 |
| e |
综上所述,g(x)≥h(x)恒成立,又因为这两个函数不在同一点取最值,
于是g(x)>h(x)恒成立,
从而 原不等式成立.
点评:本小题主要考查函数单调性的应用、利用导数研究曲线上某点切线方程、利用导数研究函数的极值、不等式的证明等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.

练习册系列答案
相关题目
函数y=2x-
的零点所在区间为( )
| 1 |
| x |
A、(0,
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
已知圆的圆心为C(-1,3),直线3x+4y-7=0被圆截得的弦长为
,则圆的方程为( )
8
| ||
| 5 |
| A、(x+1)2+(y-3)2=4 |
| B、(x-1)2+(y+3)2=4 |
| C、(x+1)2+(y+3)2=4 |
| D、(x-1)2+(y-3)2=4 |
点P是双曲线
-
=1右支上一点,F1,F2分别是该双曲线的左,右焦点,点M为线段PF2的中点.若△OMF2的面积为10,则点P到该双曲线的左准线的距离为( )
| x2 |
| 9 |
| y2 |
| 16 |
A、3
| ||||
B、3
| ||||
C、3
| ||||
D、3
|
下列计算正确的是( )
| A、a6÷a6=0 |
| B、(-bc)4÷(-bc)2=-bc |
| C、y4+y6=y10 |
| D、(ab4)4=a4b16 |