Question

在区间（0，1）内任取两个实数，则它们的和大于

1

2

而小于

3

2

的概率是

 

．

Answer 1

考点：几何概型

专题：计算题

分析：设所取的两个数分别为x，y，则

0＜x＜1 0＜y＜1

，求出基本区域的面积，然后由所取的两个数的和大于

1

2

而小于

3

2

为事件A，可得A：

0＜x＜1 0＜y＜1 1 2 ＜x+y＜ 3 2

，计算所对应的区域的面积，由几何概率的求解公式可求

解答： 解：设所取的两个数分别为x，y，则

0＜x＜1 0＜y＜1

，其对于的区域是边长为1的正方形，面积为1
记所取的两个数的和大于

1

2

而小于

3

2

为事件A，则A：

0＜x＜1 0＜y＜1 1 2 ＜x+y＜ 3 2

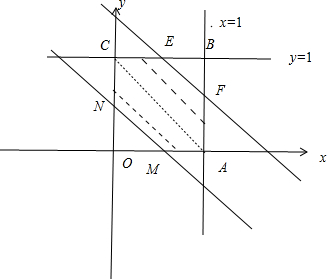
所对应的区域如图所示的阴影部分
其面积为S=1-S_△EBF-S_OMN=1-

1

2

×

1

2

×

1

2

-

1

2

×

1

2

×

1

2

=

3

4

∴P（A）=

3

4

故答案为：

3

4

点评：本题主要考查了与面积有关的几何概率的求解，解题的关键是准确求出基本事件及指导事件的面积