题目内容
3.已知函数f(x)=loga(-x-1)+loga(x+3),其中a>0且a≠1.(1)求函数f(x)的定义域;
(2)求函数f(x)的值域.
分析 (1)根据函数成立的条件即可求函数f(x)的定义域;
(2)根据对数的运算性质,以及符合函数的值域的求法,即可得到答案,需要分类讨论.
解答 解:(1)要使函数有意义,则$\left\{\begin{array}{l}{-x-1>0}\\{x+3>0}\end{array}\right.$.
解得:-3<x<-1.
即f(x)的为定义域(-3,-1),
(2)f(x)=loga(-x-1)+loga(x+3)=loga[-(x+1)(x+3)],
令t=-(x+1)(x+3),
∵-3<x<-1,
∴0<t≤1,
当0<a<1时,值域为[0,+∞),
当a>1时,值域为(-∞,0].
点评 本题主要考查对数函数性质的综合考查,根据对数函数的单调性是解决本题的关键.注意要对a进行分类讨论.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
13.已知命题p:?x∈R,|x|<0,则¬p是( )
| A. | ?x∈R,|x|≥0 | B. | ?x∈R,|x|>0 | C. | ?x∈R,|x|≥0 | D. | ?x∈R,|x|<0 |
14.如果a>b>0,那么下列不等式成立的是( )
| A. | a2>ab | B. | ab<b2 | C. | $\frac{1}{a}$>$\frac{1}{b}$ | D. | $\frac{b}{a}$>$\frac{a}{b}$ |
11.一个正三棱锥的正视图及俯视图如图所示,则该三棱锥的左视图的面积为( )
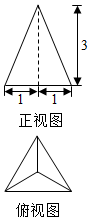

| A. | 6 | B. | $\frac{3\sqrt{3}}{2}$ | C. | $\frac{2\sqrt{21}}{3}$ | D. | $\sqrt{10}$ |
8.已知某几何体的三视图如上图所示,则该几何体的体积为( )
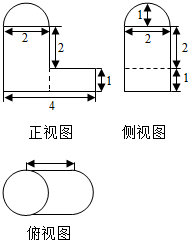

| A. | 3+$\frac{10}{3}$π | B. | 4+$\frac{11}{3}$π | C. | 3+$\frac{11}{3}$π | D. | 4+$\frac{8}{3}$π |
15.已知M={(x,y)|x2+2y2=3},N={(x,y)|y=mx+b}.若对于所有的m∈R,均有M∩N≠∅,则b的取值范围是( )
| A. | $({-\frac{{2\sqrt{3}}}{3},\frac{{2\sqrt{3}}}{3}})$ | B. | $({-\frac{{\sqrt{6}}}{2},\frac{{\sqrt{6}}}{2}})$ | C. | $[{-\frac{{\sqrt{6}}}{2},\frac{{\sqrt{6}}}{2}}]$ | D. | $[{-\frac{{2\sqrt{3}}}{3},\frac{{2\sqrt{3}}}{3}}]$ |
12.已知函数f(x)=(m+2)x2+mx+1为偶函数,则f(x)在区间(1,+∞)上是( )
| A. | 先增后减 | B. | 先减后增 | C. | 减函数 | D. | 增函数 |
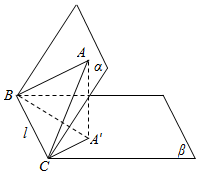 如图,已知二面角α-BC-β的大小为θ(0≤θ≤$\frac{π}{2}$).在面α内有△ABC,它在面β内的射影为△A′BC.它们的面积分别为S,S′,求证:cosθ=$\frac{S′}{S}$.
如图,已知二面角α-BC-β的大小为θ(0≤θ≤$\frac{π}{2}$).在面α内有△ABC,它在面β内的射影为△A′BC.它们的面积分别为S,S′,求证:cosθ=$\frac{S′}{S}$.