题目内容
13.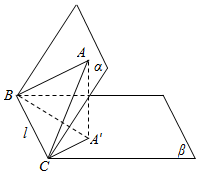 如图,已知二面角α-BC-β的大小为θ(0≤θ≤$\frac{π}{2}$).在面α内有△ABC,它在面β内的射影为△A′BC.它们的面积分别为S,S′,求证:cosθ=$\frac{S′}{S}$.
如图,已知二面角α-BC-β的大小为θ(0≤θ≤$\frac{π}{2}$).在面α内有△ABC,它在面β内的射影为△A′BC.它们的面积分别为S,S′,求证:cosθ=$\frac{S′}{S}$.
分析 根据二面角的定义结合三角形的面积公式进行证明即可.
解答 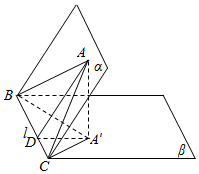 解:∵△ABC在面β内的射影为△A′BC.
解:∵△ABC在面β内的射影为△A′BC.
∴AA′⊥β,
过A作AD⊥BC,连接A′D,
∵AA′⊥BC,A′A∩AD=A,
∴BC⊥平面AA′DM
则A′D⊥BC,
即∠ADA′是面角α-BC-β的平面角,即∠ADA′=θ,
则S=$\frac{1}{2}$BC•AA′,S′=$\frac{1}{2}$BC•A′D,
则$\frac{S′}{S}$=$\frac{\frac{1}{2}BC•A′D}{\frac{1}{2}BC•A′D}$=$\frac{A′D}{AD}$,
在直角三角形AA′D中,cosθ=$\frac{A′D}{AD}$,
∴cosθ=$\frac{S′}{S}$
点评 本题主要考查二面角的应用,根据二面角的定义作出二面角的平面角,结合直角三角形的边角关系是解决本题的关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
1.函数f(x)=-4x3+6x2+1在[0,3]上的最大值为( )
| A. | 1 | B. | 3 | C. | 4 | D. | 6 |
2.$\frac{sin20°cos20°}{cos50°}$=( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
