题目内容
11.一个正三棱锥的正视图及俯视图如图所示,则该三棱锥的左视图的面积为( )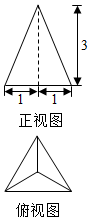
| A. | 6 | B. | $\frac{3\sqrt{3}}{2}$ | C. | $\frac{2\sqrt{21}}{3}$ | D. | $\sqrt{10}$ |
分析 由已知中的三视图可得:该几何体是一个以俯视图为底面的三棱锥,分析出左视图的形状,可得答案.
解答 解:由已知中的三视图可得:该几何体是一个以俯视图为底面的三棱锥,
其底面边长为2,高为3,
故底面的边上的高为$\sqrt{3}$,
即左视图是一个底为$\sqrt{3}$,高为3,
故左视图的面积为:$\frac{3\sqrt{3}}{2}$,
故选:B
点评 本题考查的知识点是由三视图,求体积和表面积,根据已知的三视图,判断几何体的形状是解答的关键.

练习册系列答案
相关题目
19.圆O1:x2+y2-6x-4y-3=0和圆O2:x2+y2-4y=0的位置关系是( )
| A. | 相离 | B. | 相交 | C. | 外切 | D. | 内切 |
6.某几何体的三视图如图所示,则该几何体的表面积为( )
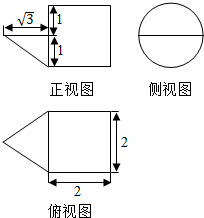

| A. | $\frac{13π}{2}+\sqrt{3}$ | B. | $\frac{(12+\sqrt{3})π}{6}$ | C. | $\frac{15π}{2}$ | D. | $\frac{(6+\sqrt{3})π}{3}$ |
1.函数f(x)=-4x3+6x2+1在[0,3]上的最大值为( )
| A. | 1 | B. | 3 | C. | 4 | D. | 6 |
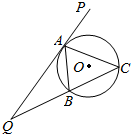 如图,△ABC的外接圆为⊙O,延长CB至Q,再延长QA至P,且QA为⊙O的切线
如图,△ABC的外接圆为⊙O,延长CB至Q,再延长QA至P,且QA为⊙O的切线 如图,已知F1(0,-1),F2(0,1)为椭圆Γ:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的两个焦点,过F1作两条倾斜角互补的直线l1,l2,l1,l2分别与椭圆Γ相交于A,B,C,D四点,且△ABF2的周长为8.
如图,已知F1(0,-1),F2(0,1)为椭圆Γ:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的两个焦点,过F1作两条倾斜角互补的直线l1,l2,l1,l2分别与椭圆Γ相交于A,B,C,D四点,且△ABF2的周长为8.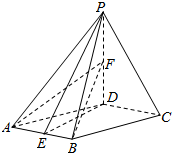 已知四棱锥P-ABCD,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PA=AD,点E为AB中点,点F在线段PD上,且PF:FD=1:3.
已知四棱锥P-ABCD,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PA=AD,点E为AB中点,点F在线段PD上,且PF:FD=1:3.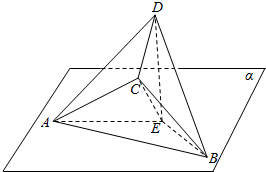 如图,三棱锥C-ABD的棱AB在平面α内,棱CD在平面α外,平面CAB⊥平面α,点D在平面α内的射影为E,且满足EA⊥EB,AC=BC=EA=EB=2,DE=2$\sqrt{2}$.
如图,三棱锥C-ABD的棱AB在平面α内,棱CD在平面α外,平面CAB⊥平面α,点D在平面α内的射影为E,且满足EA⊥EB,AC=BC=EA=EB=2,DE=2$\sqrt{2}$.