题目内容
已知i是虚数单位,若复数z满足(z-i)(3-i)=10,则|z|=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:复数求模,复数代数形式的混合运算
专题:数系的扩充和复数
分析:通过复数的乘除运算,求出复数z,然后求出复数的模即可.
解答:
解::由(z-i)(3-i)=10
得z=
+i=
+i=3+2i,
∴|z|=
=
.
故选:D.
得z=
| 10 |
| 3-i |
| 10(3+i) |
| (3-i)(3+i) |
∴|z|=
| 32+22 |
| 13 |
故选:D.
点评:本题考查复数的代数形式的混合运算,复数的模的求法,考查计算能力.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
下列命题中为真的是( )
| A、在△ABC中,a:b:c=sinA:sinB:sinC | ||
| B、常数列既是等差数列又是等比数列 | ||
C、函数y=
| ||
| D、若两个平面与第三个平面都垂直,则这两个平面平行 |
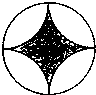 如图,将半径为l的圆分成相等的四段弧,再将四段弧围成星形放在圆内(阴影部分).现在往圆内任投一点,此点落在星形区域内的概率为( )
如图,将半径为l的圆分成相等的四段弧,再将四段弧围成星形放在圆内(阴影部分).现在往圆内任投一点,此点落在星形区域内的概率为( )A、
| ||||
B、
| ||||
C、1-
| ||||
D、
|
设x,y满足约束条件
,则目标函数z=x+2y的最大值是( )
|
| A、3 | B、4 | C、5 | D、6 |
如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为( )


| A、2 | ||
| B、1 | ||
C、
| ||
D、
|