Question

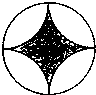如图，将半径为l的圆分成相等的四段弧，再将四段弧围成星形放在圆内（阴影部分）．现在往圆内任投一点，此点落在星形区域内的概率为（　　）

• A、

  4

  π

  -1
• B、

  1

  π

• C、1-

  1

  π

• D、

  2

  π

Answer 1

考点：几何概型

专题：概率与统计

分析：根据几何概型，求出阴影部分的面积，即可得到结论．

解答： 解：将图形平均分成四个部分，则每个图形空白处的面积为2（

1

4

×π-

1

2

×1×1）=2（

π

4

-

1

2

）=

π

2

-1，
阴影部分的面积为π×12-4(

π

2

-1)=4-π，
∴根据几何概型的概率公式可得点落在星形区域内的概率为：

4-π

π

=

4

π

-1，
故选：A．

点评：本题主要考查几何概型的概率计算，求出阴影部分的面积是解决本题的关键．