题目内容
几名大学毕业生合作开设3D打印店,生产并销售某种3D产品.已知该店每月生产的产品当月都能销售完,每件产品的生产成本为34元,该店的月总成本由两部分组成:第一部分是月销售产品的生产成本,第二部分是其它固定支出20000元.假设该产品的月销售量t(x)(件)与销售价格x(元/件)(x∈N*)之间满足如下关系:①当34≤x≤60时,t(x)=-a(x+5)2+10050;②当60≤x≤70时,t(x)=-100x+7600.设该店月利润为M(元),月利润=月销售总额-月总成本.
(1)求M关于销售价格x的函数关系式;
(2)求该打印店月利润M的最大值及此时产品的销售价格.
(1)求M关于销售价格x的函数关系式;
(2)求该打印店月利润M的最大值及此时产品的销售价格.
考点:导数在最大值、最小值问题中的应用,函数模型的选择与应用
专题:应用题,函数的性质及应用,导数的综合应用
分析:(1)利用x=60时,t(60)=1600,求出a,可得M关于销售价格x的函数关系式;
(2)利用分段函数,分别求最值,即可求该打印店月利润M的最大值及此时产品的销售价格.
(2)利用分段函数,分别求最值,即可求该打印店月利润M的最大值及此时产品的销售价格.
解答:
解:(1)当x=60时,t(60)=1600,代入t(x)=-a(x+5)2+10050,
解得a=2. …(2分)
∴M(x)=
…(4分)
(2)设g(u)=(-2u2-20u+10000)(u-34)-20000,34≤u<60,u∈R,则g′(u)=-6(u2-16u-1780).
令g′(u)=0,解得u1=8-2
(舍去),u2=8+2
∈(50,51].…(7分)
当34<u<50时,g′(u)>0,g(u)单调递增;
当51<u<60时,g′(u)<0,g(u)单调递减. …(10分)
∵x∈N*,M(50)=44000,M(51)=44226,∴M(x)的最大值为44226.…(12分)
当60≤x≤70时,M(x)=100(-x2+110x-2584)-20000单调递减,
故此时M(x)的最大值为m(60)=21600. …(14分)
综上所述,当x=51时,月利润M(x)有最大值44226元. …(15分)
答:该打印店店月利润最大为44226元,此时产品的销售价格为51元/件. …(16分)
解得a=2. …(2分)
∴M(x)=
|
(2)设g(u)=(-2u2-20u+10000)(u-34)-20000,34≤u<60,u∈R,则g′(u)=-6(u2-16u-1780).
令g′(u)=0,解得u1=8-2
| 461 |
| 461 |
当34<u<50时,g′(u)>0,g(u)单调递增;
当51<u<60时,g′(u)<0,g(u)单调递减. …(10分)
∵x∈N*,M(50)=44000,M(51)=44226,∴M(x)的最大值为44226.…(12分)
当60≤x≤70时,M(x)=100(-x2+110x-2584)-20000单调递减,
故此时M(x)的最大值为m(60)=21600. …(14分)
综上所述,当x=51时,月利润M(x)有最大值44226元. …(15分)
答:该打印店店月利润最大为44226元,此时产品的销售价格为51元/件. …(16分)
点评:本题考查函数模型的选择与应用,考查导数知识的运用,考查学生利用数学知识解决实际问题的能力,属于中档题.

练习册系列答案
相关题目
已知i是虚数单位,若复数z满足(z-i)(3-i)=10,则|z|=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知集合A={x|-1≤x≤2},B={x|x2≤4x},则A∩B=( )
| A、[-1,4] |
| B、[-1,0] |
| C、[0,2] |
| D、[0,4] |
已知m≥2,点P(x,y)满足
点Q的坐标为(0,-1),记f(m)为
•
的最小值,则f(m)的最大值为( )
|
| OP |
| OQ |
A、-
| ||
B、-
| ||
| C、0 | ||
D、
|
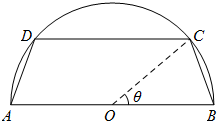 一个圆柱形圆木的底面半径为1m,长为10m,将此圆木沿轴所在的平面剖成两个部分.现要把其中一个部分加工成直四棱柱木梁,长度保持不变,底面为等腰梯形ABCD(如图所示,其中O为圆心,C,D在半圆上),设∠BOC=θ,木梁的体积为V(单位:m3),表面积为S(单位:m2).
一个圆柱形圆木的底面半径为1m,长为10m,将此圆木沿轴所在的平面剖成两个部分.现要把其中一个部分加工成直四棱柱木梁,长度保持不变,底面为等腰梯形ABCD(如图所示,其中O为圆心,C,D在半圆上),设∠BOC=θ,木梁的体积为V(单位:m3),表面积为S(单位:m2).