题目内容
设全集U=R，集合A={x|x2-2x＜0}，集合B={x|y=lg（x-1）}，则A∩B=（ ）
| A、{x|1≤x＜2} |
| B、{x|x＞2} |
| C、{x|x＞1} |
| D、{x|1＜x＜2} |
考点：交集及其运算
专题：集合
分析：求出A中不等式的解集确定出A，求出B中x的范围确定出B，找出A与B的交集即可．
解答：
解：由A中不等式变形得：x（x-2）＜0，
解得：0＜x＜2，即A={x|0＜x＜2}，
由B中y=lg（x-1），得到x-1＞0，
解得：x＞1，即B={x|x＞1}，
则A∩B={x|1＜x＜2}．
故选：D．
解得：0＜x＜2，即A={x|0＜x＜2}，
由B中y=lg（x-1），得到x-1＞0，
解得：x＞1，即B={x|x＞1}，
则A∩B={x|1＜x＜2}．
故选：D．
点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
孟建平小学滚动测试系列答案
黄冈天天练口算题卡系列答案
相关题目
从集合A={1，2，3，4，5}任意取出两个数，这两个数的和是偶数的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f（x）=x3-tx2+3x，若对于任意的a∈[1，2]，b∈（2，3]，函数f（x）在区间（a，b）上单调递减，则实数t的取值范围是（ ）
| A、（-∞，3] |
| B、（-∞，5] |
| C、[3，+∞） |
| D、[5，+∞） |
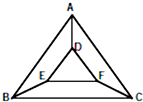如图，用四种不同颜色给图中的ABCDEF六个点涂色，要求每个点涂一种颜色，且图中每条线段的两个端点涂不同的颜色，而且四种不同颜色要全部用完，则不同的涂色方法共有（ ）种．| A、144 | B、216 |
| C、264 | D、360 |
设函数f（x）=|sin（2x+
）|，则下列关于函数f（x）的说法中正确的是（ ）
| π |
| 3 |
| A、f（x）是偶函数 | ||||
| B、f（x）最小正周期为π | ||||
C、f（x）图象关于点（-
| ||||
D、f（x）在区间[
|
将函数f（x）=2sin（
+
）的图象向左平移
个单位，再向下平移1个单位，得到函数g（x）的图象，则g（x）的解析式为（ ）
| x |
| 3 |
| π |
| 6 |
| π |
| 4 |
A、g（x）=2sin（
| ||||
B、g（x）=2sin（
| ||||
C、g（x）=2sin（
| ||||
D、g（x）=2sin（
|