题目内容
已知两点M(-1,0),N(1,0),若直线y=k(x-2)上至少存在三个点P,使得△MNP是直角三角形,则实数k的取值范围是( )
A、[-
| ||||||||
B、[-
| ||||||||
C、[-
| ||||||||
| D、[-5,5] |
考点:两条直线垂直与倾斜角、斜率的关系
专题:直线与圆
分析:当k=0时,M、N、P三点共线,构不成三角形,故k≠0.△MNP是直角三角形,由直径对的圆周角是直角,知直线和以MN为直径的圆有公共点即可,由此能求出实数k的取值范围.
解答:
解:当k=0时,M、N、P三点共线,构不成三角形,
∴k≠0,
如图所示,△MNP是直角三角形,有三种情况:
当M是直角顶点时,直线上有唯一点P1点满足条件;
当N是直角顶点时,直线上有唯一点P3满足条件;
当P是直角顶点时,此时至少有一个点P满足条件.
由直径对的圆周角是直角,知直线和以MN为直径的圆有公共点即可,
则
≤1,解得-
≤k≤
,且k≠0.
∴实数k的取值范围是[-
,0)∪(0,
].
故选:A.

∴k≠0,
如图所示,△MNP是直角三角形,有三种情况:
当M是直角顶点时,直线上有唯一点P1点满足条件;
当N是直角顶点时,直线上有唯一点P3满足条件;
当P是直角顶点时,此时至少有一个点P满足条件.
由直径对的圆周角是直角,知直线和以MN为直径的圆有公共点即可,
则
| |2k| | ||
|
| ||
| 3 |
| ||
| 3 |
∴实数k的取值范围是[-
| ||
| 3 |
| ||
| 3 |
故选:A.
点评:本题考查直线与圆的位置关系等基础知识,意在考查运用方程思想求解能力,考查数形结合思想的灵活运用.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
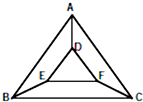 如图,用四种不同颜色给图中的ABCDEF六个点涂色,要求每个点涂一种颜色,且图中每条线段的两个端点涂不同的颜色,而且四种不同颜色要全部用完,则不同的涂色方法共有( )种.
如图,用四种不同颜色给图中的ABCDEF六个点涂色,要求每个点涂一种颜色,且图中每条线段的两个端点涂不同的颜色,而且四种不同颜色要全部用完,则不同的涂色方法共有( )种.| A、144 | B、216 |
| C、264 | D、360 |
设函数f(x)=|sin(2x+
)|,则下列关于函数f(x)的说法中正确的是( )
| π |
| 3 |
| A、f(x)是偶函数 | ||||
| B、f(x)最小正周期为π | ||||
C、f(x)图象关于点(-
| ||||
D、f(x)在区间[
|
已知条件p:函数f(x)=ax-2b+2 对于任意的x∈[-1,1]恒有f(x)≥0,若对任意的一个实数a∈[-2,2],一个实数 b∈[0,2],则满足条件P的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
下列函数中,在(0,+∞)上为减函数的是( )
A、y=
| ||
| B、y=(1-x)ex | ||
| C、y=x-ln(1+x) | ||
| D、y=x3-x |
在△ABC中,则“A=
”是“cosA=
”的( )
| π |
| 6 |
| ||
| 2 |
| A、充分必要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |
将函数f(x)=2sin(
+
)的图象向左平移
个单位,再向下平移1个单位,得到函数g(x)的图象,则g(x)的解析式为( )
| x |
| 3 |
| π |
| 6 |
| π |
| 4 |
A、g(x)=2sin(
| ||||
B、g(x)=2sin(
| ||||
C、g(x)=2sin(
| ||||
D、g(x)=2sin(
|