题目内容
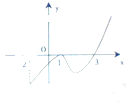 如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题:
如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题:①3是函数y=f(x)的极大值点;
②1是函数y=f(x)的极值点;
③当x>3时,f(x)>0恒成立;
④函数y=f(x)在x=-2处切线的斜率小于零;
⑤函数y=f(x)在区间(-2,3)上单调递减.
则正确命题的序号是
考点:利用导数研究函数的单调性
专题:导数的概念及应用
分析:由图象得出函数的单调区间,函数的极值点,结合函数的性质即可得出结论.
解答:
解:由图象得:
在(-2,3)上,f′(x)<0,f(x)递减,
在(3,+∞)上,f′(x)>0,f(x)递增,
∴f(x)min=f(3),
故①②③错误,④⑤正确,
故答案为:④⑤.
在(-2,3)上,f′(x)<0,f(x)递减,
在(3,+∞)上,f′(x)>0,f(x)递增,
∴f(x)min=f(3),
故①②③错误,④⑤正确,
故答案为:④⑤.
点评:本题考察了函数的单调性,导数的应用,渗透了数形结合思想,是一道基础题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
cos
的值等于( )
| 5π |
| 12 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
若变量x,y满足约束条件
,则z=3x-4y的取值范围是( )
|
| A、[-11,3] |
| B、[-11,-3] |
| C、[-3,11] |
| D、[3,11] |
设椭圆
+
=1和双曲线
-x2=1的公共焦点分别为F1、F2,P为这两条曲线的一个交点,则cos∠F1PF2的值为( )
| x2 |
| 2 |
| y2 |
| m |
| y2 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、-
|