题目内容
若函数f（x）=x3-6ax的单调递减区间是（-2，2），则a的取值范围是 ．
考点：函数的单调性与导数的关系
专题：导数的综合应用
分析：求函数的导数，根据函数单调性和导数之间的关系即可得到结论．
解答：
解：∵f（x）=x3-6ax，
∴f′（x）=3x2-6a，
∵函数f（x）=x3-6ax的单调递减区间是（-2，2），
∴x=-2或x=2是方程f′（x）=3x2-6a=0的两个根，
则3×4-6a=0，即a=2，
故答案为：{2}
∴f′（x）=3x2-6a，
∵函数f（x）=x3-6ax的单调递减区间是（-2，2），
∴x=-2或x=2是方程f′（x）=3x2-6a=0的两个根，
则3×4-6a=0，即a=2，
故答案为：{2}
点评：本题主要考查函数的单调性和导数之间的关系，比较基础．
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
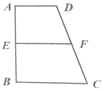如图梯形ABCD中，AD∥BC，∠ABC=90°，AD：BC：AB=2：3：4，E、F分别是AB，CD的中点，将四边形ADFE沿直线EF进行翻折．给出四个结论：
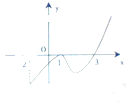如图是函数y=f（x）的导函数y=f′（x）的图象，给出下列命题：一个棱锥的三视图如图，则该棱锥的表面积为（ ）
A、48+12
| ||
B、48+24
| ||
C、72+12
| ||
D、72+24
|