题目内容
在△ABC,边a,b是方程x2-2
x+2=0的两根,角A,B满足2cos(A+B)-1=0,求角C的度数,边c的长度及△ABC的面积.
| 3 |
考点:正弦定理,余弦定理
专题:解三角形
分析:先根据2cos(A+B)-1=0求得cos(A+B)的值,进而求得A+B利用三角形内角和求得C,根据韦达定理求得a+b和ab的值,进而利用余弦定理求得c,最后利用三角形面积公式求得答案.
解答:
解:∵2cos(A+B)-1=0,
∴cos(A+B)=
,
∴A+B=
,
∴C=π-A-B=
,
∵a,b是方程x2-2
x+2=0的两根,
∴a+b=2
,ab=2,
∴cosC=
=
=
=-
,
∴c=
,
S=
absinC=
×2×
=
.
∴cos(A+B)=
| 1 |
| 2 |
∴A+B=
| π |
| 3 |
∴C=π-A-B=
| 2π |
| 3 |
∵a,b是方程x2-2
| 3 |
∴a+b=2
| 3 |
∴cosC=
| a2+b2-c2 |
| 2ab |
| (a+b)2-2ab-c2 |
| 2ab |
| 12-4-c2 |
| 4 |
| 1 |
| 2 |
∴c=
| 10 |
S=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
点评:本题主要考查了正弦定理和余弦定理的应用.考查了三角函数基础知识的综合运用.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
直线l1:x+y-2
=0与直线l2:
(t为参数)的交点到原点O的距离是( )
| 2 |
|
| A、1 | ||
B、
| ||
| C、2 | ||
D、2
|
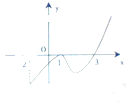 如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题:
如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题: 如图是某几何体的三视图,它的正视图和侧视图均为矩形,俯视图为正三角形(长度单位:cm)
如图是某几何体的三视图,它的正视图和侧视图均为矩形,俯视图为正三角形(长度单位:cm)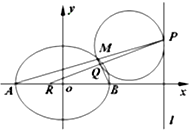 如图,A,B是椭圆C:
如图,A,B是椭圆C: