题目内容
已知椭圆
+
=1,过点(1,0)作倾斜角为45°的直线l交椭圆于A、B两点,O为坐标原点,则△AOB的面积为 .
| x2 |
| 4 |
| y2 |
| 3 |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:过点(1,0)作倾斜角为45°的直线l方程为y=x-1,联立
,得7x2-8x-8=0,由此利用韦达定理、弦长公式、点到直线距离公式能求出△AOB的面积.
|
解答:
解:过点(1,0)作倾斜角为45°的直线l方程为y=x-1,
联立
,得7x2-8x-8=0,
△=64+4×7×8>0,
设A(x1,y1),B(x2,y2),则x1+x2=
,x1x2=-
,
|AB|=
=
,
原点O(0,0)到直线y=x-1的距离d=
=
,
∴△AOB的面积S=
×d×|AB|=
×
×
=
.
故答案为:
.
联立
|
△=64+4×7×8>0,
设A(x1,y1),B(x2,y2),则x1+x2=
| 8 |
| 7 |
| 8 |
| 7 |
|AB|=
(1+1)[(
|
| 24 |
| 7 |
原点O(0,0)到直线y=x-1的距离d=
| |-1| | ||
|
| ||
| 2 |
∴△AOB的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 24 |
| 7 |
6
| ||
| 7 |
故答案为:
6
| ||
| 7 |
点评:本题考查三角形的面积的求法,是中档题,解题时要注意椭圆性质、韦达定理、弦长公式、点到直线距离公式的合理运用.

练习册系列答案
相关题目
读如图程序,当输出的值y的范围大于1时,则输入的x值的取值范围是( )
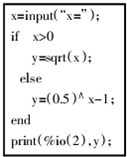
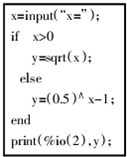
| A、(-∞,-1) |
| B、(1,+∞) |
| C、(-∞,-1)∪(1,+∞) |
| D、(-∞,0)∪(0,+∞) |
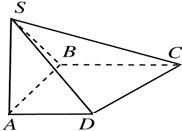 如图所示,ABCD是直角梯形,∠ABC=90°,SA⊥底面ABCD,SA=AB=BC=1,AD=
如图所示,ABCD是直角梯形,∠ABC=90°,SA⊥底面ABCD,SA=AB=BC=1,AD=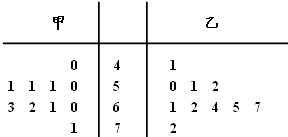 随机抽取某中学甲、乙两班各10名学生,测量他们的体重(单位:kg),获得体重数据的茎叶图如图:
随机抽取某中学甲、乙两班各10名学生,测量他们的体重(单位:kg),获得体重数据的茎叶图如图: