Question

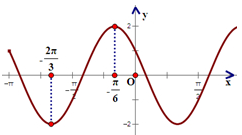如图所示为函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π）的部分图象．
（1）根据图象求函数y=f（x）的解析式．
（2）求函数y=f（x）在区间[0，

π

2

]上的值域．
（3）求出y=f（x），x∈[

π

6

，π]时的单调区间．

Answer 1

考点：由y=Asin（ωx+φ）的部分图象确定其解析式,函数y=Asin（ωx+φ）的图象变换

专题：三角函数的图像与性质

分析：（1）由图象直接得到A与T，代入周期公式求得ω，由五点作图的第二点求得φ，则函数解析式可求；
（2）直接由x∈[0，

π

2

]求得函数值域；
（3）分别求出函数f（x）的增区间与减区间，与[

π

6

，π]取交集后得答案．

解答： 解：（1）由图可知，A=2，T=2[-

π

6

-（-

2π

3

）]=π，
∴

2π

ω

=π，ω=2．
再由五点作图的第二点得，2×(-

π

6

)+φ=

π

2

，解得：φ=

5π

6

．
∴f（x）=2sin（2x+

5π

6

）；
（2）∵x∈[0，

π

2

]，
∴2x+

5π

6

∈[

5π

6

，

11π

6

]，
则2sin（2x+

5π

6

）∈[-2，1]．
即y=f（x）在区间[0，

π

2

]上的值域是[-2，1]；
（3）由-

π

2

+2kπ≤2x+

5π

6

≤

π

2

+2kπ，
解得：-

2π

3

+kπ≤x≤-

π

6

+kπ，k∈Z．
取k=1，得

π

3

≤x≤

5π

6

，
由

π

2

+2kπ≤2x+

5π

6

≤

3π

2

+2kπ，
解得：-

π

6

+kπ≤x≤

π

3

+kπ，k∈Z．
取k=0，得-

π

6

≤x≤

π

3

，
取k=1，得

5π

6

≤x≤

4π

3

．
∴y=f（x）在x∈[

π

6

，π]时的单调增区间为：[

π

3

，

5π

6

]，k∈Z；
单调减区间为：[

π

6

，

π

3

]，[

5π

6

，π]，k∈Z．

点评：本题考查由函数y=Asin（ωx+φ）的部分图象求函数解析式，考查了函数值域的求法，训练了复合函数的单调性的求法，是中档题．