题目内容
已知公差大于零的等差数列{an}的前n项和为Sn,且满足a3•a4=117,a2+a5=22,求Sn的最小值.
考点:等差数列的性质
专题:等差数列与等比数列
分析:由已知条件推导出a3,a4是一元二次方程x2-22x+117=0的两个根,且a3<a4,从而求出a3=9,a4=13,进而得到a1=1,d=4,由此能求出Sn的最小值.
解答:
解:∵公差大于零的等差数列{an}的前n项和为Sn,
且满足a3•a4=117,a2+a5=22,
∴a3+a4=a2+a5=22,
∴a3,a4是一元二次方程x2-22x+117=0的两个根,且a3<a4,
解得a3=9,a4=13,
∴
,
解得a1=1,d=4,
∴Sn=n+
•4
=2n2-n
=2(n2-
n)
=2(n-
)2-
,
∴n=1时,Sn取最小值1.
且满足a3•a4=117,a2+a5=22,
∴a3+a4=a2+a5=22,
∴a3,a4是一元二次方程x2-22x+117=0的两个根,且a3<a4,
解得a3=9,a4=13,
∴
|
解得a1=1,d=4,
∴Sn=n+
| n(n-1) |
| 2 |
=2n2-n
=2(n2-
| 1 |
| 2 |
=2(n-
| 1 |
| 4 |
| 1 |
| 8 |
∴n=1时,Sn取最小值1.
点评:本题考查数列的最小值的求法,是中档题,解题时要认真审题,注意韦达定理的合理运用.

练习册系列答案
相关题目
一个几何体的三视图如图所示,则该几何体的体积为( )


| A、55 | ||
| B、54 | ||
C、75+4
| ||
D、55+2
|
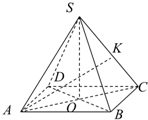 如图,设S-ABCD是一个高为3的四棱锥,底面ABCD是边长为2的正方形,顶点S在底面上的射影是正方形ABCD的中心.K是棱SC的中点.试求直线AK与平面SBC所成角的大小.
如图,设S-ABCD是一个高为3的四棱锥,底面ABCD是边长为2的正方形,顶点S在底面上的射影是正方形ABCD的中心.K是棱SC的中点.试求直线AK与平面SBC所成角的大小.