题目内容
函数f(x)=x2-4x-4在闭区间[t,t+1](t∈R)上的最小值记为g(t),
(1)当t=1时,求g(1)的值;
(2)求g(t)的解析式,并求g(t)最小值.
(1)当t=1时,求g(1)的值;
(2)求g(t)的解析式,并求g(t)最小值.
考点:函数解析式的求解及常用方法,二次函数的性质
专题:分类讨论
分析:(1)当t=1时,[t,t+1]=[1,2],利用图象可判断f(x)=x2-4x-4单调性并求出最小值.
(2)按照对称轴在的位置分三种情况进行讨论,写成分段函数,最值求解按照分段函数分段求解的思路求解.
(2)按照对称轴在的位置分三种情况进行讨论,写成分段函数,最值求解按照分段函数分段求解的思路求解.
解答:
解:函数f(x)=x2-4x-4图象开口向上,对称轴为直线x=2,
(1)当t=1时,区间[t,t+1]为[1,2],
函数在[1,2]上单调递减,最小值g(1)=f(2)=-8.
(2)当t+1≤2即t≤1时,函数在[t,t+1]单调递减,g(t)=f(t+1)=(t+1)2-4(t+1)-4=t2-2t-7;
当t<2≤t+1即1<t<2时,函数在对称轴x=2处取得最小值,g(t)=f(2)=-8,
当t≥2时,函数在[t,t+1]单调递增,g(t)=f(t)=t2-4t-4,
综上g(t)的解析式为
g(t)=t
当t≤1时,g(t)=t2-2t-7,为二次函数,图象开口向上,在t=-
=1时取得最小值g(1)=-8
当1<t<2时,g(t)=-8,
当t≥2时,g(t)=t2-2t-4,为二次函数,图象开口向上,对称轴直线为t=-
=1,函数单调递增,t=2时取得最小值g(2)=-4
综上可述,t∈R时,g(t)最小值为-8
(1)当t=1时,区间[t,t+1]为[1,2],
函数在[1,2]上单调递减,最小值g(1)=f(2)=-8.
(2)当t+1≤2即t≤1时,函数在[t,t+1]单调递减,g(t)=f(t+1)=(t+1)2-4(t+1)-4=t2-2t-7;
当t<2≤t+1即1<t<2时,函数在对称轴x=2处取得最小值,g(t)=f(2)=-8,
当t≥2时,函数在[t,t+1]单调递增,g(t)=f(t)=t2-4t-4,
综上g(t)的解析式为
g(t)=t
|
当t≤1时,g(t)=t2-2t-7,为二次函数,图象开口向上,在t=-
| -2 |
| 2×1 |
当1<t<2时,g(t)=-8,
当t≥2时,g(t)=t2-2t-4,为二次函数,图象开口向上,对称轴直线为t=-
| -2 |
| 2×1 |
综上可述,t∈R时,g(t)最小值为-8
点评:本题考查二次函数的含参讨论问题,基本上分为三种情况进行讨论,最后写成分段函数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在等腰直角△ABC中,AB=AC=3,点D在边BC上且BD=
如图,在等腰直角△ABC中,AB=AC=3,点D在边BC上且BD=| 1 |
| 2 |
| AP |
| CP |
A、[-
| ||
B、[-
| ||
C、[
| ||
D、[0,
|
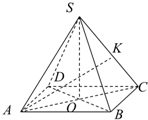 如图,设S-ABCD是一个高为3的四棱锥,底面ABCD是边长为2的正方形,顶点S在底面上的射影是正方形ABCD的中心.K是棱SC的中点.试求直线AK与平面SBC所成角的大小.
如图,设S-ABCD是一个高为3的四棱锥,底面ABCD是边长为2的正方形,顶点S在底面上的射影是正方形ABCD的中心.K是棱SC的中点.试求直线AK与平面SBC所成角的大小.