题目内容

已知非空有限实数集S的所有非空子集依次记为S1，S2，S3，…，集合Sk中所有元素的平均值记为bk．将所有bk组成数组T：b1，b2，b3，…，数组T中所有数的平均值记为m（T）．
（1）若S={1，2}，求m（T）；
（2）若S={a1，a2，…，an}（n∈N*，n≥2），求m（T）．
考点：集合的包含关系判断及应用,元素与集合关系的判断
专题：计算题
分析：（1）先求出S={1，2}的所有非空子集为{1}，{2}，{1，2}，利用m（T）的定义求出其值
（2）利用组合数及m（T）的定义求出m（T）=
n
i=1
ai+
1
2
C
1
n-1
n
i=1
ai+
1
3
C
2
n-1
n
i=1
ai+…+
1
n
C
n-1
n-1
n
i=1
ai
C
1
n
+
C
2
n
+
C
3
n
+…+
C
n
n
，利用组合数的性质，化简求值．
解答： 解：（1）S={1，2}的所有非空子集为{1}，{2}，{1，2}，
∴数组T为：1，2，
3
2

∴m（T）=
1+2+
3
2
3
=
3
2

（2）∵S={a1，a2，…，an}
∴m（T）=
n
i=1
ai+
1
2
C
1
n-1
n
i=1
ai+
1
3
C
2
n-1
n
i=1
ai+…+
1
n
C
n-1
n-1
n
i=1
ai
C
1
n
+
C
2
n
+
C
3
n
+…+
C
n
n

1+
1
2
C
1
n-1
+
1
3
C
2
n-1
+…+
1
n
C
n-1
n-1
C
1
n
+
C
2
n
+
C
3
n
+…+
C
n
n
n
i=1
ai
又∵
1
k
C
k-1
n-1
=
1
k
•
(n-1)!
(k-1)!(n-k)!
=
1
n
•
n!
(n-k)!k!
=
1
n
C
k
n

∴m（T）=
1
n
C
1
n
+
1
n
C
2
n
+
1
n
C
3
n
+…+
1
n
C
n-1
n-1
C
1
n
+
C
2
n
+
C
3
n
+…+
C
n
n
n
i=1
ai
=
1
n
n
i
ai
点评：本题考查集合的子集及组合的应用，关键是弄清楚题中对新概念的理解，属于一道难题．
练习册系列答案
相关题目
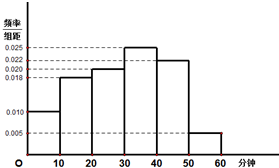电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况，随机抽取了100名观众进行调查，其中女性有55名．如图是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图；将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”，已知“体育迷”中有10名女性．
（1）根据已知条件完成下面的2×2列联表．
非体育迷 体育迷 合计
男
女
合计
（2）根据列联表的独立性检验，有多大的把握认为“体育迷”与性别有关？
（3）将日均收看该体育项目不低于50分钟的观众称为“超级体育迷”，已知“超级体育迷”中有2名女性，若从“超级体育迷”中任意选取2人，求至少有1名女性观众的概率．
参考公式：x2=
n(ad-bc)2
(a+b)(b+c)(a+c)(b+d)
（其中n=a+b+c+d）
x2≤2.706 x2＞2.706 x2＞3.841 x2＞6.635
是否有关联 没有关联 90% 95% 99%
在等差数列{an}中，已知a2=3，a5=a2+6，数列{bn}满足bn+1=2bn-1（n∈N*），且b1=3．
（Ⅰ）求通项公式an，bn；
（Ⅱ）设数列{
2
an•an+1
}的前n项和为Sn，试比较Sn与1-
1
bn
的大小．
计算：
（1）已知tanα=2，求4sin2α+2sinαcosα的值．
（2）已知sinα=
2
5
5
，且α在第二象限，求tan（α+3π）+
sin(
9π
2
+α)
cos(
9π
2
-α)
的值．
设函数f（x）=ax-（k-1）a-x（a＞0且a≠1）是定义域为R的奇函数．
（Ⅰ）求k的值；
（Ⅱ）若f（1）=
3
2
，且g（x）=[f（x）-2m]•2x在[0，+∞）上的最小值为-5，求m的值．
求由曲线y=
x
，y=2-x，y=-
1
3
x围成图形的面积．
求曲线y=x2与直线y=x，y=2x所围成的图形的面积．
已知数列{An}：a1，a2，a3，…，an（n∈N*，n≥2）满足a1=an=0，且当2≤k≤n（k∈N）时，（ak-ak-1）2=1，记S（An）=
n
i=1
ai．
（Ⅰ）写出S（A5）的所有可能的值；      
（Ⅱ）求S（An）的最大值．
若正实数x，y满足x+2y+4=4xy，且不等式（x+2y）a2+2a+2xy-34≥0恒成立，则实数a的取值范围是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网