题目内容
在等差数列{an}中,已知a2=3,a5=a2+6,数列{bn}满足bn+1=2bn-1(n∈N*),且b1=3.
(Ⅰ)求通项公式an,bn;
(Ⅱ)设数列{
}的前n项和为Sn,试比较Sn与1-
的大小.
(Ⅰ)求通项公式an,bn;
(Ⅱ)设数列{
| 2 |
| an•an+1 |
| 1 |
| bn |
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(Ⅰ)由已知条件求出公差d=2,由此能求出an=2n-1.由已知条件推导出{bn-1}是首项为2,公比为2的等比数列.由此能求出bn=2n+1.
(Ⅱ)由
=
-
,利用裂项求和法求出Sn=1-
,再由作差法能比较Sn与1-
的大小.
(Ⅱ)由
| 2 |
| an •an+2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| 1 |
| 2n+1 |
| 1 |
| bn |
解答:
解:(Ⅰ) 因为a5-a2=3d=6,所以d=2.
所以an=a2+(n-2)d=3+2(n-2)=2n-1.…(3分)
因为bn+1=2bn-1(n∈N*),所以bn+1-1=2(bn-1).
所以{bn-1}是首项为2,公比为2的等比数列.
所以bn-1=2•2n-1=2n.
故bn=2n+1.…(6分)
(Ⅱ)
=
=
-
.…(7分)
所以Sn=
-
+
-
+…
-
=1-
.…(9分)
从而Sn-(1-
)=1-
-1+
=
-
=
.…(10分)
故当n=1,2时,2n=2n,Sn=1-
.
当n≥3时,2n<2n,Sn<1-
.…(14分)
所以an=a2+(n-2)d=3+2(n-2)=2n-1.…(3分)
因为bn+1=2bn-1(n∈N*),所以bn+1-1=2(bn-1).
所以{bn-1}是首项为2,公比为2的等比数列.
所以bn-1=2•2n-1=2n.
故bn=2n+1.…(6分)
(Ⅱ)
| 2 |
| an •an+2 |
| 2 |
| (2n-1)(2n+1) |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
所以Sn=
| 1 |
| 1 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| 1 |
| 2n+1 |
从而Sn-(1-
| 1 |
| bn |
| 1 |
| 2n+1 |
| 1 |
| 2n+1 |
| 1 |
| 2n+1 |
| 1 |
| 2n+1 |
| 2n-2n |
| (2n+1)(2n+1) |
故当n=1,2时,2n=2n,Sn=1-
| 1 |
| bn |
当n≥3时,2n<2n,Sn<1-
| 1 |
| bn |
点评:本题主要考查等差、等比数列的概念,通项公式及求和公式等基础知识,同时考查运算求解能力.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
质点做直线运动,其速度v(t)=3t2-2t+3,则它在第2秒内所走的路程为( )
| A、1 | B、3 | C、5 | D、7 |
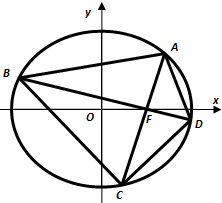 已知椭圆Γ:
已知椭圆Γ: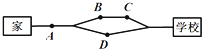 小明早上从家里出发到学校上课,如图所示,有两条路线可走,且走哪条路线的可能性是相同的,图中A、B、C、D处都有红绿灯,小明在每个红绿灯处遇到红灯的概率都是
小明早上从家里出发到学校上课,如图所示,有两条路线可走,且走哪条路线的可能性是相同的,图中A、B、C、D处都有红绿灯,小明在每个红绿灯处遇到红灯的概率都是 四棱锥S-ABCD,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知∠DAB=135°,BC=2
四棱锥S-ABCD,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知∠DAB=135°,BC=2