题目内容
若正实数x,y满足x+2y+4=4xy,且不等式(x+2y)a2+2a+2xy-34≥0恒成立,则实数a的取值范围是 .
考点:基本不等式
专题:不等式的解法及应用
分析:原不等式恒成立可化为xy≥
恒成立,由基本不等式结合不等式的解法可得xy≥2,故只需2≥
恒成立,解关于a的不等式可得.
| 2a2-a+17 |
| 2a2+1 |
| 2a2-a+17 |
| 2a2+1 |
解答:
解:∵正实数x,y满足x+2y+4=4xy,可得x+2y=4xy-4,
∴不等式(x+2y)a2+2a+2xy-34≥0恒成立,
即(4xy-4)a2+2a+2xy-34≥0恒成立,
变形可得2xy(2a2+1)≥4a2-2a+34恒成立,
即xy≥
恒成立,
∵x>0,y>0,∴x+2y≥2
,
∴4xy=x+2y+4≥4+2
,
即2(
)2-
•
-2≥0,解不等式可得
≥
,或
≤-
(舍负)
可得xy≥2,要使xy≥
恒成立,只需2≥
恒成立,
化简可得2a2+a-15≥0,
即(a+3)(2a-5)≥0,解得a≤-3或a≥
,
故答案为:(-∞,-3]∪[
,+∞)
∴不等式(x+2y)a2+2a+2xy-34≥0恒成立,
即(4xy-4)a2+2a+2xy-34≥0恒成立,
变形可得2xy(2a2+1)≥4a2-2a+34恒成立,
即xy≥
| 2a2-a+17 |
| 2a2+1 |
∵x>0,y>0,∴x+2y≥2
| 2xy |
∴4xy=x+2y+4≥4+2
| 2xy |
即2(
| xy |
| 2 |
| xy |
| xy |
| 2 |
| xy |
| ||
| 2 |
可得xy≥2,要使xy≥
| 2a2-a+17 |
| 2a2+1 |
| 2a2-a+17 |
| 2a2+1 |
化简可得2a2+a-15≥0,
即(a+3)(2a-5)≥0,解得a≤-3或a≥
| 5 |
| 2 |
故答案为:(-∞,-3]∪[
| 5 |
| 2 |
点评:本题考查基本不等式的应用,涉及恒成立问题,变形并求出需要的最小值是解决问题的关键,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
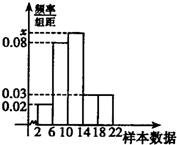 为了调查学生每天零花钱的数量(钱数取整数元),以便引导学生树立正确的消费观.样本容量1000的频率分布直方图如图所示,则样本数据落在[6,14)内的频数为( )
为了调查学生每天零花钱的数量(钱数取整数元),以便引导学生树立正确的消费观.样本容量1000的频率分布直方图如图所示,则样本数据落在[6,14)内的频数为( )| A、780 | B、660 |
| C、680 | D、460 |