题目内容
设函数f(x)=ax-(k-1)a-x(a>0且a≠1)是定义域为R的奇函数.
(Ⅰ)求k的值;
(Ⅱ)若f(1)=
,且g(x)=[f(x)-2m]•2x在[0,+∞)上的最小值为-5,求m的值.
(Ⅰ)求k的值;
(Ⅱ)若f(1)=
| 3 |
| 2 |
考点:指数函数综合题
专题:函数的性质及应用
分析:(Ⅰ)根据函数奇偶性的性质建立方程关系,即可求k的值;
(Ⅱ)利用换元法,结合指数函数的性质建立方程关系即可求出m的值.
(Ⅱ)利用换元法,结合指数函数的性质建立方程关系即可求出m的值.
解答:
解:(Ⅰ)由题意,对任意x∈R,f(-x)=-f(x),
即a-x-(k-1)ax=-ax+(k-1)a-x,
即(k-1)(ax+a-x)-(ax+a-x)=0,(k-2)(ax+a-x)=0,
因为x为任意实数,所以k=2.
(Ⅱ)由(Ⅰ)f(x)=ax-a-x,因为f(1)=
,所以a-
=
,解得a=2.
故f(x)=2x-2-x,g(x)=[f(x)-2m]•2x=(2x)2-2m•2x-1,
令t=2x,由x∈[0,+∞),得t∈[1,+∞),
所以g(x)=h(t)=t2-2mt-1=(t-m)2-m2-1,t∈[1,+∞),
当m<1时,h(t)在[1,+∞)上是增函数,
则h(t)min=h(1)=-2m=-5,
解得m=
(舍去).
当m≥1时,则h(t)min=-m2-1=-5,解得m=2,或m=-2(舍去).
综上,m的值是2.
即a-x-(k-1)ax=-ax+(k-1)a-x,
即(k-1)(ax+a-x)-(ax+a-x)=0,(k-2)(ax+a-x)=0,
因为x为任意实数,所以k=2.
(Ⅱ)由(Ⅰ)f(x)=ax-a-x,因为f(1)=
| 3 |
| 2 |
| 1 |
| a |
| 3 |
| 2 |
故f(x)=2x-2-x,g(x)=[f(x)-2m]•2x=(2x)2-2m•2x-1,
令t=2x,由x∈[0,+∞),得t∈[1,+∞),
所以g(x)=h(t)=t2-2mt-1=(t-m)2-m2-1,t∈[1,+∞),
当m<1时,h(t)在[1,+∞)上是增函数,
则h(t)min=h(1)=-2m=-5,
解得m=
| 5 |
| 2 |
当m≥1时,则h(t)min=-m2-1=-5,解得m=2,或m=-2(舍去).
综上,m的值是2.
点评:本题主要考查函数奇偶性的应用以及指数函数的图象和性质,考查学生的计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 四棱锥S-ABCD,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知∠DAB=135°,BC=2
四棱锥S-ABCD,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知∠DAB=135°,BC=2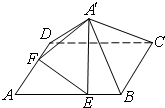 如图,已知正方形ABCD的边长为6,点E,F分别在边AB,AD上,AE=AF=4,现将△AEF沿线段EF折起到△A′EF位置,使得A′C=2
如图,已知正方形ABCD的边长为6,点E,F分别在边AB,AD上,AE=AF=4,现将△AEF沿线段EF折起到△A′EF位置,使得A′C=2