题目内容
计算:
(1)已知tanα=2,求4sin2α+2sinαcosα的值.
(2)已知sinα=
,且α在第二象限,求tan(α+3π)+
的值.
(1)已知tanα=2,求4sin2α+2sinαcosα的值.
(2)已知sinα=
2
| ||
| 5 |
sin(
| ||
cos(
|
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:(1)原式分母看做“1”,利用同角三角函数间基本关系变形后,将tanα的值代入计算即可求出值;
(2)由sinα的值及α的范围,利用同角三角函数间基本关系求出cosα的值,原式利用诱导公式化简后,再利用同角三角函数间基本关系变形,将各自的值代入计算即可求出值.
(2)由sinα的值及α的范围,利用同角三角函数间基本关系求出cosα的值,原式利用诱导公式化简后,再利用同角三角函数间基本关系变形,将各自的值代入计算即可求出值.
解答:
解:(1)∵tanα=2,
∴原式=
=
=
=4;
(2)∵sinα=
,且α在第二象限,
∴cosα=-
=-
,
则原式=tanα+
=
+
=-2-
=-2
.
∴原式=
| 4sin2α+2sinαcosα |
| sin2α+cos2α |
| 4tan2α+2tanα |
| tan2α+1 |
| 16+4 |
| 4+1 |
(2)∵sinα=
2
| ||
| 5 |
∴cosα=-
| 1-sin2α |
| ||
| 5 |
则原式=tanα+
| cosα |
| sinα |
| sinα |
| cosα |
| cosα |
| sinα |
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
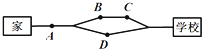 小明早上从家里出发到学校上课,如图所示,有两条路线可走,且走哪条路线的可能性是相同的,图中A、B、C、D处都有红绿灯,小明在每个红绿灯处遇到红灯的概率都是
小明早上从家里出发到学校上课,如图所示,有两条路线可走,且走哪条路线的可能性是相同的,图中A、B、C、D处都有红绿灯,小明在每个红绿灯处遇到红灯的概率都是