题目内容
已知f(x)是二次函数,若f(0)=0,且f(x+1)=f(x)+x+1.
(1)求函数f(x)的解析式;
(2)求函数y=f(x2-2)的值域.
(1)设f(x)=ax2+bx+c(a≠0),
又f(0)=0,∴c=0,即f(x)=ax2+bx.
又f(x+1)=f(x)+x+1.
∴a(x+1)2+b(x+1)=ax2+bx+x+1.
∴(2a+b)x+a+b=(b+1)x+1,
∴
∴f(x)=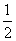 x2+
x2+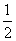 x.
x.
(2)由(1)知y=f(x2-2)=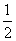 (x2-2)2+
(x2-2)2+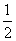 (x2-2)
(x2-2)
=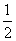 (x4-3x2+2)=
(x4-3x2+2)=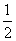 (x2-
(x2- )2-
)2- ,
,
当x2= 时,y取最小值-
时,y取最小值- .
.
∴函数y=f(x2-2)的值域为[- ,+∞).
,+∞).

练习册系列答案
相关题目
 ,又记f1(x)=f(x),fk+1(x)=f(fk(x)),k=1,2,…,则f2015(x)=( )
,又记f1(x)=f(x),fk+1(x)=f(fk(x)),k=1,2,…,则f2015(x)=( )

 的定义域是________.
的定义域是________. 若f(1)+f(a)=2,则a的所有可能值为( )
若f(1)+f(a)=2,则a的所有可能值为( )