题目内容
求cos
cos
cos
cos
cos
= .
| π |
| 11 |
| 2π |
| 11 |
| 3π |
| 11 |
| 4π |
| 11 |
| 5π |
| 11 |
考点:二倍角的正弦
专题:三角函数的求值
分析:利用诱导公式、二倍角公式把要求的式子化为=
,计算求得结果.
| ||||
16sin
|
解答:
解:cos
cos
cos
cos
cos
=-cos
cos
cos
cos
cos
=
=
=
=
=
,
故答案为:
.
| π |
| 11 |
| 2π |
| 11 |
| 3π |
| 11 |
| 4π |
| 11 |
| 5π |
| 11 |
| π |
| 11 |
| 2π |
| 11 |
| 8π |
| 11 |
| 4π |
| 11 |
| 5π |
| 11 |
=
2sin
| ||||||||||||
2sin
|
| ||||||
2sin
|
=
-sin
| ||||
16sin
|
| ||||
16sin
|
| 1 |
| 32 |
故答案为:
| 1 |
| 32 |
点评:本题主要考查诱导公式、二倍角公式的应用,属于中档题.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
某四面体的三视图均为直角三角形,如图,则该四面体的表面积为( )

A、72+24
| ||
B、96+24
| ||
| C、126 | ||
| D、64 |
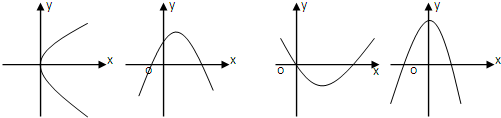
在下面的四个图象中,其中一个图象是函f(x)=
x3+ax2+(a2-1)x+1(a∈R)的导函数y=f′(x)的图象,则f(-1)等于( )
| 1 |
| 3 |

A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|