题目内容

方程x2-sinx=0的根有
 
个．
考点：正弦函数的图象
专题：函数的性质及应用
分析：由x2-sinx=0得x2=sinx，作出函数y=x2和sinx的图象，根据图象利用数形结合即可得到结论．
解答： 解：由x2-sinx=0得x2=sinx，作出函数y=x2和sinx的图象，
由图象可知，两个函数的交点个数为2个，
故方程根的个数为2，
故答案为：2
点评：本题主要考查方程根的个数的应用，利用数形结合是解决本题的关键．将方程转化为函数，利用数形结合是解决此类问题的基本方法．
练习册系列答案
相关题目
已知f（x）=aln（x-1），g（x）=x2+bx，F（x）=f（x+1）-g（x），其中a，b∈R．
（I）若y=f（x）与y=g（x）的图象在交点（2，k）处的切线互相垂直，求a，b的值；
（Ⅱ）当b=2-a，a＞0时，求F（x）的最大值；
（Ⅲ）若x=2是函数F（x）的一个极值点，x0和1是F（x）的两个零点，且x0∈（n，n+1），n∈N，求n．
已知等差数列{an}中，a1=1，前n项和为Sn且满足条件：
S2n
Sn
=
4n+2
n+1
（n∈N*）
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）若数列{bn}的前n项和为Tn有
Tn+1-bn+1
Tn+bn
=1（n∈N*），b1=3，又cn=
2an+1
bn-1
，求数列{cn}的前n项和Wn．
已知复数Z的实部大于0且满足|Z|=
2
，Z2的虚部为2，
（1）求Z；
（2）设Z，Z2，Z-Z2在复平面对应的点分别为A，B，C求△ABC的面积．
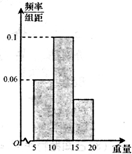如图是一容量为100的样本的重量的频率分布直方图，样本重量均在[5，20]内，其分组为[5，10），[10，15），[15，20]，则样本重量落在[15，20]内的频数为
 
．
已知函数f（x）=
.
11
12x
.
，则f-1（1）=
 
．
已知f（x）是定义在R上的奇函数，当x≥0时，f（x）=-x2-2x，若f（2-a2）＞f（a），则实数a的取值范围是
 
．
求cos
π
11
cos
2π
11
cos
3π
11
cos
4π
11
cos
5π
11
=
 
．
点P是圆C：（x-3）2+（y+4）2=4上的动点，点O为坐标原点，则|OP|的最大值为（　　）
A、5B、6C、7D、8

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网