题目内容
若sin（
+α）=
，则sin（
+2α）= ．
| π |
| 3 |
| 1 |
| 3 |
| π |
| 6 |
考点：两角和与差的正弦函数,二倍角的正弦
专题：三角函数的求值
分析：由二倍角公式可得cos（
+2α）的值，由诱导公式可得sin（
+2α）=-cos（
+2α），代入可得．
| 2π |
| 3 |
| π |
| 6 |
| 2π |
| 3 |
解答：
解：∵sin（
+α）=
，∴cos2（
+α）=1-2sin2（
+α），
即cos（
+2α）=1-2sin2（
+α）=
，
∴sin（
+2α）=-cos[
+（
+2α）]
=-cos（
+2α）=-
故答案为：-
| π |
| 3 |
| 1 |
| 3 |
| π |
| 3 |
| π |
| 3 |
即cos（
| 2π |
| 3 |
| π |
| 3 |
| 7 |
| 9 |
∴sin（
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
=-cos（
| 2π |
| 3 |
| 7 |
| 9 |
故答案为：-
| 7 |
| 9 |
点评：本题考查两角和与差的正弦公式和二倍角公式，以及诱导公式的应用，属中档题．
练习册系列答案
中考解读考点精练系列答案
相关题目
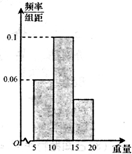如图是一容量为100的样本的重量的频率分布直方图，样本重量均在[5，20]内，其分组为[5，10），[10，15），[15，20]，则样本重量落在[15，20]内的频数为已知变量x，y具有线性相关关系，测得（x，y）的一组数据如下：（0，1），（1，2），（2，4），（3，5），其回归方程为
=1.4x+a，则a的值等于（ ）
 |
| y |
| A、0.9 | B、0.8 |
| C、0.6 | D、0.2 |