题目内容
已知a，b∈R，i是虚数，若a-2bi与1+4i互为共轭复数，则|a+bi|= ．
考点：复数求模
专题：数系的扩充和复数
分析：利用复数的模的计算公式、共轭复数的定义即可得出
解答：
解：∵a-2bi与1+4i互为共轭复数，
∴a=1，-2b+4=0，
解得a=1，b=2．
∴|a+bi|=|1+2i|=
=
．
故答案为：
．
∴a=1，-2b+4=0，
解得a=1，b=2．
∴|a+bi|=|1+2i|=
| 12+22 |
| 5 |
故答案为：
| 5 |
点评：本题考查了复数的模的计算公式、共轭复数的定义，属于基础题．
练习册系列答案
相关题目
在△ABC中，角A，B，C所对的边分别是a，b，c，已知A=60°，C=45°，c=10，则a=（ ）
| A、6 | ||||
| B、8 | ||||
C、5
| ||||
D、
|
若复数z与2+3i互为共轭复数，则复数z的模|z|=（ ）
A、
| ||
| B、5 | ||
| C、7 | ||
| D、13 |
复数
为纯虚数，则实数a=（ ）
| a+i |
| 2-i |
| A、-2 | ||
B、-
| ||
| C、2 | ||
D、
|
函数f（x）=(x-5)0+(x-2)-
的定义域是（ ）
| 1 |
| 3 |
| A、{x|x∈R且x≠5，x≠2} |
| B、{x|x＞2} |
| C、{x|x＞5} |
| D、{x|2＜x＜5或x＞5} |
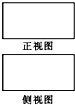如图是长和宽分别相等的两个矩形，给定下列四个命题：