题目内容
在平面直角坐标系中，已知角α的终边经过点P（a，a-3），且cosα=
，则a=（ ）
| ||
| 5 |
| A、1 | ||
B、
| ||
C、1或
| ||
| D、1或3 |
考点：任意角的三角函数的定义
专题：三角函数的求值
分析：利用三角函数的定义，直接列出关系式求出a的值．
解答：
解：角α的终边经过点P（a，a-3），且cosα=
，
所以a＞0，并且
=
，
解得a=1．
故选：A．
| ||
| 5 |
所以a＞0，并且
| a | ||
|
| ||
| 5 |
解得a=1．
故选：A．
点评：本题考查三角函数的定义的应用，考查计算能力．
练习册系列答案
轻松暑假总复习系列答案
相关题目
△ABC中sin2A-sin2B-sin2C≥
sinBsinC时，角A的取值范围是（ ）
| 3 |
A、（0，
| ||
B、[
| ||
C、[
| ||
D、[0，
|
函数f（x）=
的定义域为（ ）
log
|
| A、（-∞，1] | ||
| B、[1，+∞） | ||
C、（
| ||
D、（
|
二项式（2x+
）7的展开式中
的系数是（ ）
| 1 |
| x |
| 1 |
| x3 |
| A、42 | B、168 | C、84 | D、21 |
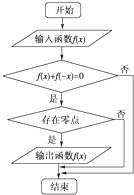
某流程图如图所示，现输入如下四个函数，则可以输出的函数是（ ）
| A、f（x）=sinx | ||
| B、f（x）=cosx | ||
C、f（x）=
| ||
| D、f（x）=x2 |
已知△ABC中，a、b分别是角A、B所对的边，且a=x（x＞0），b=2，A=60°，若三角形有两解，则x的取值范围是（ ）
A、x＞
| ||
| B、0＜x＜2 | ||
C、
| ||
D、
|
将函数f（x）=sinx+cosx的图象向左平移φ（φ＞0）个单位长度，所得图象关于原点对称，则φ的最小值为（ ）
A、-
| ||
B、
| ||
C、
| ||
D、
|
极坐标方程ρcos2θ=4sin θ所表示的曲线是（ ）
| A、一条直线 | B、一个圆 |
| C、一条抛物线 | D、一条双曲线 |