题目内容
20.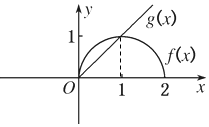 已知y=f(x)是偶函数,y=g(x)是奇函数,它们的定义域均为[-2,2],且它们在x∈[0,2]上图象如图所示,f(x)>g(x)的解集是( )
已知y=f(x)是偶函数,y=g(x)是奇函数,它们的定义域均为[-2,2],且它们在x∈[0,2]上图象如图所示,f(x)>g(x)的解集是( )| A. | [-2,0)∪(0,1) | B. | (0,1) | C. | [-2,0) | D. | (-2,0)∪(0,1) |
分析 根据题意,由函数的奇偶性的性质分析可得f(x)在区间[-2,0),有f(x)≥0成立,而g(x)在区间[-2,0)上,有g(x)<0恒成立,分析可得在区间[-2,0)上,都有f(x)>g(x)成立,结合图象分析可得在区间(0,1]上,f(x)>g(x)成立,综合即可得答案.
解答 解:根据题意,由图象可得:y=f(x)和y=g(x)在区间(0,2]上有f(x)≥0恒成立,
又由y=f(x)是偶函数,则f(x)在区间[-2,0),有f(x)≥0成立,
y=g(x)在区间(0,2]上有g(x)>0恒成立,
y=g(x)是奇函数,则g(x)在区间[-2,0)上,有g(x)<0恒成立,
则在区间[-2,0)上,都有f(x)>g(x)成立;
由图象可得:在区间(0,1]上,f(x)>g(x)成立,
综合可得:f(x)>g(x)的解集是[-2,0)∪(0,1);
故选:A.
点评 本题考查函数奇偶性的性质涉及函数图象的性质,关键是利用函数的奇偶性分析函数在[-2,0]上的性质.

练习册系列答案
相关题目
11.已知$sinα=\frac{4}{5},α∈({\frac{π}{2},π}),cosβ=-\frac{5}{13},β是第三象限角$.
(1)求sin(α-β)的值
(2)求tan(α+β)的值.
(1)求sin(α-β)的值
(2)求tan(α+β)的值.
15.数列{an}的前几项为$\frac{1}{2},3,\frac{11}{2},8,\frac{21}{2}…$,则此数列的通项可能是( )
| A. | ${a_n}=\frac{5n-4}{2}$ | B. | ${a_n}=\frac{3n-2}{2}$ | C. | ${a_n}=\frac{6n-5}{2}$ | D. | ${a_n}=\frac{10n-9}{2}$ |
5.一质点直线运动的方程为s=t2+1,则在时间[1,2]内的平均速度为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
12.已知α是第二象限角,sin α=$\frac{5}{13}$,则tan α=( )
| A. | -$\frac{5}{12}$ | B. | $\frac{5}{12}$ | C. | -$\frac{12}{5}$ | D. | $\frac{12}{5}$ |