题目内容
11.已知$sinα=\frac{4}{5},α∈({\frac{π}{2},π}),cosβ=-\frac{5}{13},β是第三象限角$.(1)求sin(α-β)的值
(2)求tan(α+β)的值.
分析 (1)由已知利用同角三角函数基本关系式可求cosα,sinβ,利用两角差的正弦函数公式可求sin(α-β)的值.
(2)利用同角三角函数基本关系式可求tan$α=\frac{sinα}{cosα}$=-$\frac{4}{3}$,tan$β=\frac{sinβ}{cosβ}$=$\frac{12}{5}$,利用两角和的正切函数公式即可计算得解.
解答 (本题满分为12分)
解:(1)∵$sinα=\frac{4}{5},α∈({\frac{π}{2},π}),cosβ=-\frac{5}{13},β是第三象限角$
∴cosα=-$\sqrt{1-si{n}^{2}α}$=-$\frac{3}{5}$,sinβ=-$\sqrt{1-co{s}^{2}β}$=-$\frac{12}{13}$,
∴sin(α-β)=sinαcosβ-cosαsinβ=$\frac{4}{5}×(-\frac{5}{13})-(-\frac{3}{5})×(-\frac{12}{13})$=-$\frac{56}{65}$…(6分)
(2)∵tan$α=\frac{sinα}{cosα}$=-$\frac{4}{3}$,tan$β=\frac{sinβ}{cosβ}$=$\frac{12}{5}$,
∴tan(α+β)=$\frac{tanα+tanβ}{1-tanαtanβ}$=$\frac{16}{63}$…(6分)
点评 本题主要考查了同角三角函数基本关系式,两角差的正弦函数公式,两角和的正切函数公式在三角函数化简求值中的应用,考查了转化思想,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.对任意|m|≤2,不等式x2+mx+1>2x+m恒成立,则x的取值范围为( )
| A. | x>3或x<-1 | B. | x>3 | C. | x<-1 | D. | -1<x<3 |
6.一个三位自然数abc的百位,十位,个位上的数字依次为a,b,c,当且仅当a<b且c<b时称为“凸数”.若a,b,c∈{5,6,7,8,9},且a,b,c互不相同,任取一个三位数abc,则它为“凸数”的概率是( )
| A. | $\frac{2}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{3}$ |
16.已知F1,F2分别是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的左、右焦点,两条渐近线分别为l1,l2,经过右焦点F2垂直于l1的直线分别交l1,l2于A,B两点,若|OA|+|OB|=2|AB|,且F2在线段AB上,则双曲线的渐近线斜率为( )
| A. | $±\frac{{\sqrt{5}}}{2}$ | B. | ±2 | C. | $±\sqrt{2}$ | D. | $±\frac{1}{2}$ |
20.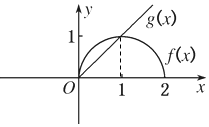 已知y=f(x)是偶函数,y=g(x)是奇函数,它们的定义域均为[-2,2],且它们在x∈[0,2]上图象如图所示,f(x)>g(x)的解集是( )
已知y=f(x)是偶函数,y=g(x)是奇函数,它们的定义域均为[-2,2],且它们在x∈[0,2]上图象如图所示,f(x)>g(x)的解集是( )
 已知y=f(x)是偶函数,y=g(x)是奇函数,它们的定义域均为[-2,2],且它们在x∈[0,2]上图象如图所示,f(x)>g(x)的解集是( )
已知y=f(x)是偶函数,y=g(x)是奇函数,它们的定义域均为[-2,2],且它们在x∈[0,2]上图象如图所示,f(x)>g(x)的解集是( )| A. | [-2,0)∪(0,1) | B. | (0,1) | C. | [-2,0) | D. | (-2,0)∪(0,1) |
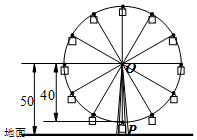 如图,某公园摩天轮的半径为40m,点O距地面的高度为50m,摩天轮做匀速转动,每3min转一圈,摩天轮上的点P的起始位置在最低点处.
如图,某公园摩天轮的半径为40m,点O距地面的高度为50m,摩天轮做匀速转动,每3min转一圈,摩天轮上的点P的起始位置在最低点处.