题目内容
10.已知偶函数f(x)在[0,+∞)上是单调函数,且图象经过A(0,-1),B(3,1)两点,f(x)<1的解集为(-3,3) .分析 根据函数f(x)的图象经过A(0,-1),B(3,1)两点可知f(0)=-1,f(3)=1,根据函数f(x)为偶函数则f(-3)=f(3)=1,函数f(x)在(-∞,0]上是减函数,然后讨论x的正负,根据函数单调性解不等式即可.
解答 解:∵函数f(x)的图象经过A(0,-1),B(3,1)两点
∴f(0)=-1,f(3)=1
设x≥0,则f(x)<1=f(3)
∵函数f(x)在[0,+∞)上是增函数
∴0≤x<3
∵函数f(x)为偶函数
∴f(-3)=f(3)=1,函数f(x)在(-∞,0]上是减函数
设x<0,则f(x)<1=f(-3)
∴-3<x<0
综上所述:f(x)<1的解集为(-3,3);
故答案为:(-3,3).
点评 本题主要考查了抽象函数的单调性和奇偶性,以及抽象函数与不等式的综合,关键是分析函数在[0,+∞)的单调性.

练习册系列答案
相关题目
17.有甲、乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表.已知从全部105人中随机抽取1人为优秀的概率为$\frac{2}{7}$.
(1)请完成上面的列联表:若按95%的可靠性要求,根据列联表的数据,能否认为“成绩与班级有关系”;
(2)若按下面的方法从甲班优秀的学生中抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号.试求抽到10号的概率.
附:${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$
(1)请完成上面的列联表:若按95%的可靠性要求,根据列联表的数据,能否认为“成绩与班级有关系”;
(2)若按下面的方法从甲班优秀的学生中抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号.试求抽到10号的概率.
| 优秀 | 非优秀 | 总计 | |
| 甲班 | 10 | 45 | 55 |
| 乙班 | 20 | 30 | 50 |
| 合计 | 30 | 75 | 105 |
| P(K2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
15.一动圆M与圆M1:(x+1)2+y2=1外切,与圆M2:(x-1)2+y2=9内切,则动圆圆心M点的轨迹方程为( )
| A. | $\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1 | B. | $\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1(x≠±2) | C. | $\frac{{x}^{2}}{16}+\frac{{y}^{2}}{15}$=1 | D. | $\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1(x≠-2) |
2.对任意|m|≤2,不等式x2+mx+1>2x+m恒成立,则x的取值范围为( )
| A. | x>3或x<-1 | B. | x>3 | C. | x<-1 | D. | -1<x<3 |
20.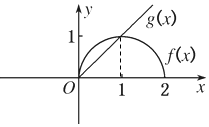 已知y=f(x)是偶函数,y=g(x)是奇函数,它们的定义域均为[-2,2],且它们在x∈[0,2]上图象如图所示,f(x)>g(x)的解集是( )
已知y=f(x)是偶函数,y=g(x)是奇函数,它们的定义域均为[-2,2],且它们在x∈[0,2]上图象如图所示,f(x)>g(x)的解集是( )
 已知y=f(x)是偶函数,y=g(x)是奇函数,它们的定义域均为[-2,2],且它们在x∈[0,2]上图象如图所示,f(x)>g(x)的解集是( )
已知y=f(x)是偶函数,y=g(x)是奇函数,它们的定义域均为[-2,2],且它们在x∈[0,2]上图象如图所示,f(x)>g(x)的解集是( )| A. | [-2,0)∪(0,1) | B. | (0,1) | C. | [-2,0) | D. | (-2,0)∪(0,1) |