题目内容
10.在△ABC中,AB=4,AC=3,$\overrightarrow{AC}$•$\overrightarrow{BC}$=1,则BC=3.分析 运用向量数量积的定义和余弦定理,解方程可得BC的长.
解答 解:由AB=4,AC=3,$\overrightarrow{AC}$•$\overrightarrow{BC}$=1,
可得|$\overrightarrow{AC}$|•|$\overrightarrow{BC}$|cosC=3|$\overrightarrow{BC}$|•$\frac{|\overrightarrow{AC}{|}^{2}+|\overrightarrow{BC}{|}^{2}-|\overrightarrow{AB}{|}^{2}}{2|\overrightarrow{AC}|•|\overrightarrow{BC}|}$=1,
即有2|$\overrightarrow{AC}$|=3(|$\overrightarrow{AC}$|2+|$\overrightarrow{BC}$|2-|$\overrightarrow{AB}$|2),
即为6=3(9+|$\overrightarrow{BC}$|2-16),
解得|$\overrightarrow{BC}$|=3,
故答案为:3.
点评 本题考查向量数量积的定义和解三角形的余弦定理的运用,考查运算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.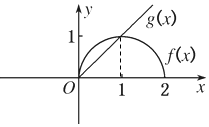 已知y=f(x)是偶函数,y=g(x)是奇函数,它们的定义域均为[-2,2],且它们在x∈[0,2]上图象如图所示,f(x)>g(x)的解集是( )
已知y=f(x)是偶函数,y=g(x)是奇函数,它们的定义域均为[-2,2],且它们在x∈[0,2]上图象如图所示,f(x)>g(x)的解集是( )
 已知y=f(x)是偶函数,y=g(x)是奇函数,它们的定义域均为[-2,2],且它们在x∈[0,2]上图象如图所示,f(x)>g(x)的解集是( )
已知y=f(x)是偶函数,y=g(x)是奇函数,它们的定义域均为[-2,2],且它们在x∈[0,2]上图象如图所示,f(x)>g(x)的解集是( )| A. | [-2,0)∪(0,1) | B. | (0,1) | C. | [-2,0) | D. | (-2,0)∪(0,1) |
5.已知函数$y=sin\frac{x}{2}+\sqrt{3}cos\frac{x}{2},x∈R$.的最大值为( )
| A. | 1+$\sqrt{3}$ | B. | 2 | C. | 1 | D. | $\sqrt{3}+\frac{1}{2}$ |
15.简单随机抽样是逐个不放回的抽样,则某一个个体被抽中的可能性( )
| A. | 与第几次抽样无关,每次抽中的可能性相等 | |
| B. | 与第几次抽样无关,第一次抽中的可能性要大些 | |
| C. | 与第几次抽样有关,最后一次抽中的可能性大些 | |
| D. | 与第几次抽样有关,虽然每次都是等可能的抽取,但各次抽取的可能性不一样 |
2.已知an=$\frac{n-\sqrt{2017}}{n-\sqrt{2016}}$ ( n∈N*),则在数列{an}的前100项中最小项和最大项分别是( )
| A. | a1,a100 | B. | a100,a44 | C. | a45,a44 | D. | a44,a45 |
19.下列函数中只有一个零点的是( )
| A. | y=x-1 | B. | y=x2-1 | C. | y=2x | D. | y=lgx |