题目内容
已知logm4<logn4,比较m与n的大小.
考点:对数函数的单调性与特殊点
专题:函数的性质及应用
分析:依题意,分m∈(0,1),n∈(0,1);m>1,n>1与n>1>m>0三类讨论,即可比较m与n的大小.
解答:
解:若m∈(0,1),n∈(0,1),则logm4<0,logn4<0,
由logm4<logn4<0得:-logm4>-logn4>0,即log
4>log
4>0,
∴1<
<
,
∴1>m>n>0;
若m>1,n>1,则logm4>0,logn4>0,
∵logm4<logn4,
∴m>n>1;
若n>1>m>0,则logm4<0<logn4显然成立,
综上所述,0<n<m,或m>n>1,或0<m<1<n.
由logm4<logn4<0得:-logm4>-logn4>0,即log
| 1 |
| m |
| 1 |
| n |
∴1<
| 1 |
| m |
| 1 |
| n |
∴1>m>n>0;
若m>1,n>1,则logm4>0,logn4>0,
∵logm4<logn4,
∴m>n>1;
若n>1>m>0,则logm4<0<logn4显然成立,
综上所述,0<n<m,或m>n>1,或0<m<1<n.
点评:本题考查对数函数的单调性与特殊点,着重考分类讨论思想与运算求解能力,属于中档题.

练习册系列答案
相关题目
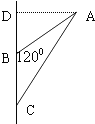 在△ABC中,AB=2,BC=1.5,∠ABC=120°(如图),若将△ABC绕直线BC旋转一周,则所形成的旋转体的体积是( )
在△ABC中,AB=2,BC=1.5,∠ABC=120°(如图),若将△ABC绕直线BC旋转一周,则所形成的旋转体的体积是( )A、
| ||
B、
| ||
C、
| ||
D、
|
在△ABC中,a2-c2+b2=-
ab,则角C=( )
| 3 |
| A、150° | B、60° |
| C、30° | D、45°或135° |
设等差数列{an}的前n项和为Sn,若S3=12,S6=42,则a10+a11+a12=( )
| A、156 | B、102 |
| C、66 | D、48 |
已知不等式2x2+mx+n>0的解集是{x|x>3或x<-2},则m+n的值是( )
| A、-14 | B、12 |
| C、-12 | D、14 |
P,Q分别为直线3x+4y-12=0与6x+8y+5=0上任意一点,则|PQ|的最小值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|