Question

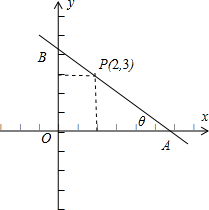
过点P（2，3）作直线l分别与x轴的正半轴和y轴的正半轴交于A（a，0），B（0，b）两点
（1）求|PA|+|PB|的最小值．
（2）当△AOB（O为原点）的面积S最小时，求直线l的方程，并求出S的最小值．
（3）当|PA|•|PB|取得最小值时，求直线?的方程．（提示：设∠OAB=θ，以θ为参变量求解，x+y-5=0）

Answer 1

考点：直线的参数方程,直线的截距式方程

专题：不等式的解法及应用,直线与圆

分析：（1）由截距式写出过A、B两点的直线方程，结合直线过定点P的关系式，求出|PA|+|PB|的最小值；
（2）写出△AOB的面积S=

1

2

ab，结合直线过定点P的关系式，求出S的最小值；
（3）设出直线?的方程

x

a

+

y

b

=1（a＞0、b＞0），∠BAO=θ，求出|PA|、|PB|的表达式；
再求|PA|•|PB|取最小值时a、b满足的条件是什么，从而求出对应直线?的方程．

解答： 解：（1）∵过A、B两点的直线方程为

x

a

+

y

b

=1（a＞0，b＞0）；
且点P在直线AB上，∴

2

a

+

3

b

=1；
∴|PA|+|PB|=

a2+b2

≥

2ab

，
当且仅当a=b时，此时

2

a

+

3

a

=1，
∴a=b=5时，取“=”；
∴|PA|+|PB|的最小值是5

2

；
（2）△AOB的面积为S=

1

2

ab，
∵

2

a

+

3

b

=1，
∴2

2 a • 3 b

≤

2

a

+

3

b

=1，
∴ab≥24，当且仅当

2

a

=

3

b

，
即a=4、b=6时取“=”；
∴a=4，b=6时，△AOB的面积取得最小值S=12；
（3）设?：

x

a

+

y

b

=1（a＞0、b＞0），∠BAO=θ，如图所示；

则|PA|=

3

sinθ

，|PB|=

b-3

sinθ

，
sinθ=

b

a2+b2

；
∴|PA|•|PB|=

3(b-3)(a2+b2)

b2

=3（b-3）[(

a

b

)2+1]；
又P（2，3）在?上，∴

2

a

+

3

b

=1；
∴

a

b

=

a-2

3

，
∴|PA|•|PB|=3（

3a

a-2

-3）[(

a-2

3

)2+1]=3×

6

a-2

×[

(a-2)2

9

+1]；
设a-2=t（t＞0），则|PA|•|PB|=

18

t

（

t2

9

+1）=2（t+

9

t

）≥12，
当且仅当t=

9

t

，即t=3时“=”成立，这时a=b=5；
∴直线?的方程为：x+y-5=0．

点评：本题考查了直线方程的应用问题，也考查了基本不等式的应用问题，考查了转化思想的应用问题，是综合性题目，属于难题．