题目内容
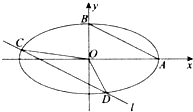 如图,A、B是椭圆
如图,A、B是椭圆| x2 |
| a2 |
| y2 |
| b2 |
| 5 |
| 1 |
| 2 |
(Ⅰ)求椭圆的方程;
(Ⅱ)设直线l平行与AB,并与椭圆相交于C、D两点,求△OCD的面积的最大值.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由已知条件推导出|AB|=
=
,k=
=-
=-
,由此能求出椭圆的方程.
(Ⅱ)设直线l的方程为y=-
x+m,将其代入
+y2=1,消去y并整理,得2x2-4mx+4m2-4=0,设C(x1,y1),D(x2,y2),则
,由此利用点到直线的距离公式和配方法能求出△OCD的面积的最大值.
| a2+b2 |
| 5 |
| b-0 |
| 0-a |
| b |
| a |
| 1 |
| 2 |
(Ⅱ)设直线l的方程为y=-
| 1 |
| 2 |
| x2 |
| 4 |
|
解答:
解:(Ⅰ)∵A、B是椭圆
+
=1(a>b>0)的两个顶点,
|AB|=
,直线AB的斜率为-
,
∴A(a,0),B(0,b),|AB|=
=
,
k=
=-
=-
,
解得a=2,b=1,
∴椭圆的方程为
+y2=1.
(Ⅱ)∵l∥AB,∴设直线l的方程为y=-
x+m,
将其代入
+y2=1,消去y并整理,得2x2-4mx+4m2-4=0,
设C(x1,y1),D(x2,y2),则
,
|CD|=
=
•|x1-x2|,
∵|x1-x2|=
2
,
∴|CD|=
•
,
点O到直线CD的距离d=
,
∴△OCD的面积S=
|CD|•d=
•
•
•
=|m|
=
,
令m2=n,则0<n<2,2m2-n4=-n2+2n=-(n-1)2+1≤1,
∴△OCD的面积的最大值为1.
| x2 |
| a2 |
| y2 |
| b2 |
|AB|=
| 5 |
| 1 |
| 2 |
∴A(a,0),B(0,b),|AB|=
| a2+b2 |
| 5 |
k=
| b-0 |
| 0-a |
| b |
| a |
| 1 |
| 2 |
解得a=2,b=1,
∴椭圆的方程为
| x2 |
| 4 |
(Ⅱ)∵l∥AB,∴设直线l的方程为y=-
| 1 |
| 2 |
将其代入
| x2 |
| 4 |
设C(x1,y1),D(x2,y2),则
|
|CD|=
(x1-x2)2+
|
1+
|
∵|x1-x2|=
| (x1+x2)2-4x1x2 |
| 2-m2 |
∴|CD|=
| 5 |
| 2-m2 |
点O到直线CD的距离d=
| |2m| | ||
|
∴△OCD的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2-m2 |
| |2m| | ||
|
=|m|
| 2-m2 |
| 2m2-m 4 |
令m2=n,则0<n<2,2m2-n4=-n2+2n=-(n-1)2+1≤1,
∴△OCD的面积的最大值为1.
点评:本题考查椭圆方程的求法,考查三角形面积的最大值的求法,解题时要认真审题,注意点到直线的距离公式和配方法的合理运用.

练习册系列答案
相关题目
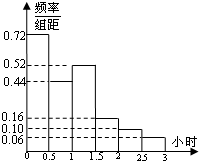 电视传媒为了解某市100万观众对足球节目的收视情况,随机抽取了100名观众进行调查.如图是根据调查结果绘制的观众每周平均收看足球节目时间的频率分布直方图,将每周平均收看足球节目时间不低于1.5小时的观众称为“足球迷”,并将其中每周平均收看足球节目时间不低于2.5小时的观众称为“铁杆足球迷”.
电视传媒为了解某市100万观众对足球节目的收视情况,随机抽取了100名观众进行调查.如图是根据调查结果绘制的观众每周平均收看足球节目时间的频率分布直方图,将每周平均收看足球节目时间不低于1.5小时的观众称为“足球迷”,并将其中每周平均收看足球节目时间不低于2.5小时的观众称为“铁杆足球迷”. 已知椭圆E:
已知椭圆E: