题目内容
f(x)定义域为(0,+∞),且满足f(x)-2x•f(
)+3x2=0,求f(x)=?
| 1 |
| x |
考点:函数解析式的求解及常用方法
专题:函数的性质及应用
分析:用
替换已知式子的x可得f(
)-2
•f(x)+3
=0,联立已知式子消去f(
)可得所求.
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x2 |
| 1 |
| x |
解答:
解:由题意用
替换已知式子的x可得f(
)-2
•f(x)+3
=0,
联立已知式子消去f(
)可得f(x)=x2+
,
∴f(x)=x2+
,x∈(0,+∞).
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x2 |
联立已知式子消去f(
| 1 |
| x |
| 2 |
| x |
∴f(x)=x2+
| 2 |
| x |
点评:本题考查函数解析式的求解,由已知式子的对称性得出f(
)-2
•f(x)+3
=0是解决问题的关键,属基础题.
| 1 |
| x |
| 1 |
| x |
| 1 |
| x2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知x,y满足不等式
,设z=
,则z的最大值与最小值的差为( )
|
| y |
| x |
| A、4 | B、3 | C、2 | D、1 |
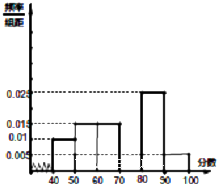 某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),[90,100]后画出如下部分频率颁布直方图,观察图形的信息,回答下列问题:
某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),[90,100]后画出如下部分频率颁布直方图,观察图形的信息,回答下列问题: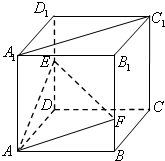 如图,在棱长为a的正方体ABCD-A1B1C1D1中,点E是棱D1D的中点,点F在棱B1B上,且满足B1F=2FB.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,点E是棱D1D的中点,点F在棱B1B上,且满足B1F=2FB.