题目内容
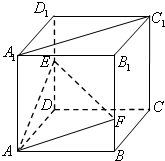 如图,在棱长为a的正方体ABCD-A1B1C1D1中,点E是棱D1D的中点,点F在棱B1B上,且满足B1F=2FB.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,点E是棱D1D的中点,点F在棱B1B上,且满足B1F=2FB.(1)求证:EF⊥A1C1;
(2)在棱C1C上确定一点G,使A,E,G,F四点共面,并求此时C1G的长;
(3)求平面AEF与平面ABCD所成二面角的余弦值.
考点:与二面角有关的立体几何综合题,空间中直线与平面之间的位置关系
专题:空间位置关系与距离,空间角
分析:(1)连结B1D1,BD,由已知条件推导出A1C1⊥DD1,从而得到A1C1⊥平面BB1D1D.由此能证明EF⊥A1C1.
(2)以点D为坐标原点,以DA,DC,DD1所在的直线分别为x轴,y轴,z轴,建立空间直角坐标系,利用向量法能求出当C1G=
a时,A,E,G,F四点共面.
(3)利用已知条件求出平面AEF的法向量和平面ABCD的一个法向量,由此能求出平面AEF与平面PQ所成二面角的余弦值.
(2)以点D为坐标原点,以DA,DC,DD1所在的直线分别为x轴,y轴,z轴,建立空间直角坐标系,利用向量法能求出当C1G=
| 1 |
| 6 |
(3)利用已知条件求出平面AEF的法向量和平面ABCD的一个法向量,由此能求出平面AEF与平面PQ所成二面角的余弦值.
解答:
(1)证明:连结B1D1,BD,∵四边形A1B1C1D1是正方形,∴B1D1⊥A1C1.
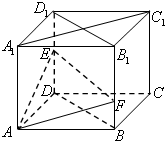 在正方体ABCD-A1B1C1D1中,
在正方体ABCD-A1B1C1D1中,
∵DD1⊥平面A1B1C1D1,A1C1?平面A1B1C1D1,∴A1C1⊥DD1.
∵B1D1∩DD1=D1,B1D1,DD1?平面BB1D1D,∴A1C1⊥平面BB1D1D.
∵EF?平面BB1D1D,∴EF⊥A1C1.
(2)解:以点D为坐标原点,
以DA,DC,DD1所在的直线分别为x轴,y轴,z轴,
建立如图的空间直角坐标系,
 则A(a,0,0),A1(a,0,a),C1(0,a,a),E(0,0,
则A(a,0,0),A1(a,0,a),C1(0,a,a),E(0,0,
a),F(a,a,
a),
∴
=(-a,a,0),
=(a,a,-
a).
设G(0,a,h),
∵平面ADD1A1∥平面BCC1B1,平面ADD1A1∩平面AEGF=AE,
平面BCC1B1∩平面AEGF=FG,
∴存在实数λ,使得
=λ
.
∵
=(-a,0,
a),
=(-a,0,h-
a),
∴(-a,0,h-
a)=λ(-a,0,
a).
∴λ=1,h=
a.∴C1G=CC1-CG=a-
a=
a.
∴当C1G=
a时,A,E,G,F四点共面.
(3)解:由(1)知
=(-a,0,
a),
=(0,a,
a).
设
=(x,y,z)是平面AEF的法向量,
则
,即
取z=6,则x=3,y=-2.
所以
=(3,-2,6)是平面AEF的一个法向量.
而
=(0,0,a)是平面ABCD的一个法向量,
设平面AEF与平面ABCD所成的二面角为θ,
则cosθ=
=
.
故平面AEF与平面PQ所成二面角的余弦值为
.
 在正方体ABCD-A1B1C1D1中,
在正方体ABCD-A1B1C1D1中,∵DD1⊥平面A1B1C1D1,A1C1?平面A1B1C1D1,∴A1C1⊥DD1.
∵B1D1∩DD1=D1,B1D1,DD1?平面BB1D1D,∴A1C1⊥平面BB1D1D.
∵EF?平面BB1D1D,∴EF⊥A1C1.
(2)解:以点D为坐标原点,
以DA,DC,DD1所在的直线分别为x轴,y轴,z轴,
建立如图的空间直角坐标系,
 则A(a,0,0),A1(a,0,a),C1(0,a,a),E(0,0,
则A(a,0,0),A1(a,0,a),C1(0,a,a),E(0,0,| 1 |
| 2 |
| 1 |
| 3 |
∴
| A1C1 |
| EF |
| 1 |
| 6 |
设G(0,a,h),
∵平面ADD1A1∥平面BCC1B1,平面ADD1A1∩平面AEGF=AE,
平面BCC1B1∩平面AEGF=FG,
∴存在实数λ,使得
| FG |
| AE |
∵
| AE |
| 1 |
| 2 |
| FG |
| 1 |
| 3 |
∴(-a,0,h-
| 1 |
| 3 |
| 1 |
| 2 |
∴λ=1,h=
| 5 |
| 6 |
| 5 |
| 6 |
| 1 |
| 6 |
∴当C1G=
| 1 |
| 6 |
(3)解:由(1)知
| AE |
| 1 |
| 2 |
| AF |
| 1 |
| 3 |
设
| n |
则
|
|
所以
| n |
而
| DD1 |
设平面AEF与平面ABCD所成的二面角为θ,
则cosθ=
| |0×3+0×(-2)+a×6| | ||
|
| 6 |
| 7 |
故平面AEF与平面PQ所成二面角的余弦值为
| 6 |
| 7 |
点评:本小题主要考查空间线面关系、四点共面、二面角的平面角、空间向量及坐标运算等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力

练习册系列答案
相关题目
半径为1的球的内接正三棱柱(底面是正三角形的直棱柱)的侧面积为3
,则正三棱柱的高为( )
| 3 |
A、2
| ||
B、
| ||
C、2
| ||
D、
|
若复数z满足z=i(2+4i)(i是虚数单位),则在复平面内,z对应的点的坐标是( )
| A、(-4,2) |
| B、(-2,4) |
| C、(2,4) |
| D、(4,2) |
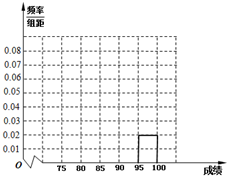 某高中毕业学年,在高校自主招生期间,把学生的平时成绩按“百分制”折算,排出前n名学生,并对这n名学生按成绩分组,第一组[75,80),第二组[80,85),第三组[85,90),第四组[90,95),第五组[95,100],如图为频率分布直方图的一部分,其中第五组、第一组、第四组、第二组、第三组的人数依次成等差数列,且第四组的人数为60.
某高中毕业学年,在高校自主招生期间,把学生的平时成绩按“百分制”折算,排出前n名学生,并对这n名学生按成绩分组,第一组[75,80),第二组[80,85),第三组[85,90),第四组[90,95),第五组[95,100],如图为频率分布直方图的一部分,其中第五组、第一组、第四组、第二组、第三组的人数依次成等差数列,且第四组的人数为60.