Question

已知x，y满足不等式

4x-y+2≥0 2x+y-8≥0 x≤2

，设z=

y

x

，则z的最大值与最小值的差为（　　）

• A、4
• B、3
• C、2
• D、1

Answer 1

考点：简单线性规划

专题：不等式的解法及应用

分析：作出不等式组对应的平面区域，z的几何意义为过原点的直线的斜率，根据数形结合即可得到结论．

解答： 解：作出不等式组对应的平面区域，如图：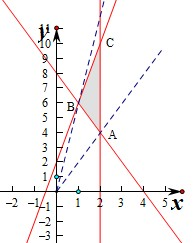
z的几何意义为过原点的直线的斜率，
则当直线经过点A时，OA的斜率最小，
经过点B时，OB的斜率最大，
由

x=2 2x+y-8=0

，解得

x=2 y=4

，此时A（2，4），即z的最小值为

4

2

=2，
由

4x-y+2=0 2x+y-8=0

，解得

x=1 y=6

，此时B（1，6），即z的最大值为

6

1

=6，
∴z的最大值与最小值的差为6-2=4，
故选：A．

点评：本题主要考查线性规划的应用以及直线斜率公式的应用，利用数形结合是解决本题的关键．