题目内容

四棱锥P-ABCD的所有侧棱长都为
3
，底面ABCD是边长2的正方形，则CD与PA所成角的余弦值
 
．
考点：异面直线及其所成的角
专题：计算题,空间角
分析：根据CD∥AB，∠PAB或其补角就是异面直线CD与PA所成的角，在△PAB中求出∠PAB的余弦值，即可得出CD与PA所成角的余弦值．
解答： 解：∵正方形ABCD中，CD∥AB
∴∠PAB或其补角就是异面直线CD与PA所成的角
△PAB中，PA=PB=
3
，AB=2
∴cos∠PAB=
3+4-3
2•
3
•2
=
3
3
．
即CD与PA所成角的余弦值为
3
3
．
故答案为：
3
3
．
点评：本题在正四棱锥中，求相对的棱所成角的余弦之值，着重考查了正四棱锥的性质和异面直线所成角求法等知识，属于基础题．
练习册系列答案
相关题目
已知A1，A2双曲线C：
x2
a2
-
y2
b2
=1（a＞0，b＞0）的顶点，B为双曲线C的虚轴一个端点．若△A1BA2是等边三角形，则双曲线C的离心率e等于
 
．
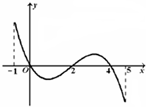已知函数y=f（x）的定义域为[-1，5]，部分对应值如下表，y=f（x）的导函数y=f′（x）的图象如图所示．下列关于y=f（x）的命题：
x-1045
f（x）1221
①函数y=f′（x）极大值点x0∈（2，4）
②函数y=f（x）的极小值点有两个
③函数y=f（x）在[0，2]上是减函数；
④函数y=f（x）的图象与x轴有2个交点
其中正确命题的序号是
 
．
若集合A={0，m2}，B={1，2}，则“m=1”是“A∪B={0，1，2}”的
 
条件．
已知C点在⊙O直径BE的延长线上，CA切⊙O于点A，若AB=AC，则
AC
BC
=
 
．
二次函数f（x）=ax2-2ax+c在区间[0，1]上单调递减，且f（m）≤f（0），则实数m的取值范围
 
．
已知等差数列{an}的前n项和为Sn，若
OB
=a1
OA
+a2014
OC
，且A、B、C三点共线（该直线不过点O），则S2014=
 
．
由两曲线y=sinx（x∈[0，2π]）和y=cosx（x∈[0，2π]）所围成的封闭图形的面积为
 
．
已知函数f（x）=3x3-ax2+x-5在区间[1，2]上单调递减，则a的取值范围是（　　）
A、[5，
37
4
]
B、（-∞，5）∪（
37
4
，+∞）
C、[5，+∞）
D、[
37
4
，+∞）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网