题目内容
已知函数f(x)=ax2+bx+1(a,b为实数,a≠0,x∈R).
(1)若函数f(x)的图象过点(-2,1),且方程f(x)=0有且只有一个根,求f(x)的表达式;
(2)在(1)的条件下,当x∈[-1,2]时,g(x)=f(x)-kx是单调函数,求实数k的取值范围.
(1)若函数f(x)的图象过点(-2,1),且方程f(x)=0有且只有一个根,求f(x)的表达式;
(2)在(1)的条件下,当x∈[-1,2]时,g(x)=f(x)-kx是单调函数,求实数k的取值范围.
考点:二次函数的性质
专题:函数的性质及应用
分析:(1)因为f(-2)=1,得b=2a.由方程f(x)=0有且只有一个根,即△=b2-4a=0,得a=1,b=2,故可求得f(x)=(x+1)2.
(2)先根据已知求得g(x)=(x-
)2+1-
,故可由二次函数的图象和性质求得实数k的取值范围.
(2)先根据已知求得g(x)=(x-
| k-2 |
| 2 |
| (k-2)2 |
| 4 |
解答:
解:(1)因为f(-2)=1,即4a-2b+1=1,所以b=2a.
因为方程f(x)=0有且只有一个根,即△=b2-4a=0.
所以4a2-4a=0.即a=1,b=2.
所以f(x)=(x+1)2.
(2)因为g(x)=f(x)-kx=x2+2x+1-kx=x2-(k-2)x+1
=(x-
)2+1-
.
所以当
≥2或
≤-1时,即k≥6或k≤0时,g(x)是单调函数.
因为方程f(x)=0有且只有一个根,即△=b2-4a=0.
所以4a2-4a=0.即a=1,b=2.
所以f(x)=(x+1)2.
(2)因为g(x)=f(x)-kx=x2+2x+1-kx=x2-(k-2)x+1
=(x-
| k-2 |
| 2 |
| (k-2)2 |
| 4 |
所以当
| k-2 |
| 2 |
| k-2 |
| 2 |
点评:本题主要考察了二次函数的性质,属于基础题.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
下列选项中是单调函数的为( )
| A、y=tanx | ||
B、y=x-
| ||
| C、y=lg(2x+1) | ||
| D、y=2|x| |
已知关于x的方程2sin(x+
)-a=0在区间[0,2π]上有两个不同的实根,则实数a的数值范围是( )
| π |
| 3 |
| A、(-2,2) | ||||
| B、[-2,2] | ||||
C、[-2,
| ||||
D、(-2,
|
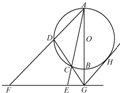 如图,AB是圆O的直径,G是AB延长线上的一点,GCD是圆O的割线,过点G作AG的垂线,交直线AC于点E,交直线 AD于点F,过点G作圆O的切线,切点为H.
如图,AB是圆O的直径,G是AB延长线上的一点,GCD是圆O的割线,过点G作AG的垂线,交直线AC于点E,交直线 AD于点F,过点G作圆O的切线,切点为H.