题目内容
椭圆
+
=1上一点P到右焦点F2的距离为b(b>1),P到左准线的距离是 .
| x2 |
| 4b2 |
| y2 |
| b2 |
考点:椭圆的标准方程
专题:圆锥曲线的定义、性质与方程
分析:先根据椭圆方程求得椭圆的半焦距c,进而可求得离心率和准线方程,进而根据椭圆的第二定义求得点P到右准线的距离,最后由两准线的距离减去P到右准线的距离即是点P到左准线的距离.
解答:
解:根据椭圆的第二定义可知P到F2的距离与其到准线的距离之比为离心率,
依题意可知a=2b,
∴c=
b,e=
=
,准线方程为x=±
=±
∴P到椭圆右准线的距离为
=
∴点P到椭圆右准线的距离
-
=2
b
故答案为:2
b
依题意可知a=2b,
∴c=
| 3 |
| c |
| a |
| ||
| 2 |
| a2 |
| c |
4
| ||
| 3 |
∴P到椭圆右准线的距离为
| b |
| e |
2
| ||
| 3 |
∴点P到椭圆右准线的距离
8
| ||
| 3 |
2
| ||
| 3 |
| 3 |
故答案为:2
| 3 |
点评:本题主要考查了椭圆的简单性质,解题的关键是灵活利用椭圆的第二定义.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
若圆(x-3)2+(y+5)2=r2上的点到直线4x-3y-2=0的最近距离等于1,则半径r的值为( )
| A、4 | B、5 | C、6 | D、9 |
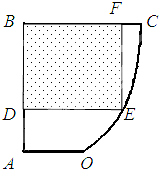 某同学的数学研究性学习课题是:在校内一块不规则土地OABC(测绘图如图所示)规划一个矩形运动场地.经过测量发现AB⊥BC,OA∥BC,曲线段OC可近似看作是以点O为顶点且开口向上的抛物线的一段,OA=20m,AB=BC=40m.
某同学的数学研究性学习课题是:在校内一块不规则土地OABC(测绘图如图所示)规划一个矩形运动场地.经过测量发现AB⊥BC,OA∥BC,曲线段OC可近似看作是以点O为顶点且开口向上的抛物线的一段,OA=20m,AB=BC=40m.