题目内容
7.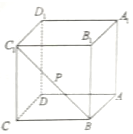 如图,点P是正方体ABCD-A1B1C1D1的面对角线BC1(线段BC1)上运动,给出下列五个命题:
如图,点P是正方体ABCD-A1B1C1D1的面对角线BC1(线段BC1)上运动,给出下列五个命题:①三棱锥A-D1PC的体积不变;
②直线AP与平面ACD1所成角的大小不变;
③二面角P-AD1-C的大小不变;
④直线AD与直线B1P为异面直线;
⑤点M是平面A1B1C1D1上到点D和C1距离相等的点,则点M一定在直线A1D1上.
其中真命题的编号为①③④⑤.(写出所有真命题的编号)
分析 对于①:容易证明AD1∥BC1,从而BC1∥平面AD1C,以P为顶点,平面AD1C为底面,易得;
对于②:可以从向量的角度进行判断;
对于③:平面PD1A平面ACD1的法向量的夹角是不变的,得到结论;
对于④:根据异面直线的判定定理,可得结论;
对于⑤:点M到点D和C1距离相等,故点M在平面A1D1CB上,进而可得结论.
解答 解:对于①:容易证明AD1∥BC1,从而BC1∥平面AD1C,
故BC1上任意一点到平面AD1C的距离均相等,所以以P为顶点,平面AD1C为底面,
则三棱锥A-D1PC的体积不变;①正确;
对于②:∵随着P点的移动,$\overrightarrow{AP}$与平面ACD1的法向量的夹角也是变化的,∴②错误
对于③:∵平面PD1A平面ACD1的法向量的夹角是不变的,∴③正确;
对于④:AD∥平面B1C1CB,B1P?平面B1C1CB,B1P与AD不平行,故直线AD与直线B1P为异面直线;④正确;
对于⑤,点M到点D和C1距离相等,故点M在平面A1D1CB上,又由M在平面A1B1C1D1上,故点M一定在直线A1D1上.故⑤正确.
故答案为:①③④⑤
点评 本题考查三棱锥体积求法中的等体积法;线面平行、垂直的判定,要注意使用转化的思想.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.直线m,n满足m?α,n?α,则n⊥m是n⊥α( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
2.已知方程x2+y2+4x-2y-4=0,则x2+y2的最大值是( )
| A. | $6\sqrt{5}$ | B. | $3+\sqrt{5}$ | C. | $14+6\sqrt{5}$ | D. | 14 |
12.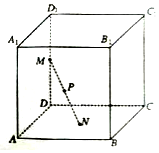 如图,已知正方体ABCD-A1B1C1D1的棱长为1,长为1的线段MN的一个端点M在棱DD1上运动,点N在正方形ABCD内运动,则MN中点P的轨迹的面积为( )
如图,已知正方体ABCD-A1B1C1D1的棱长为1,长为1的线段MN的一个端点M在棱DD1上运动,点N在正方形ABCD内运动,则MN中点P的轨迹的面积为( )
 如图,已知正方体ABCD-A1B1C1D1的棱长为1,长为1的线段MN的一个端点M在棱DD1上运动,点N在正方形ABCD内运动,则MN中点P的轨迹的面积为( )
如图,已知正方体ABCD-A1B1C1D1的棱长为1,长为1的线段MN的一个端点M在棱DD1上运动,点N在正方形ABCD内运动,则MN中点P的轨迹的面积为( )| A. | $\frac{π}{2}$ | B. | $\frac{π}{16}$ | C. | $\frac{π}{8}$ | D. | $\frac{π}{4}$ |
19.已知数列{an}的首项a1=1,对?n∈N*,都有an+1-an≤3n,an+2-an≥4•3n成立,则a2017=( )
| A. | 32017-1 | B. | $\frac{{3}^{2017}-1}{2}$ | C. | 32017+1 | D. | $\frac{{3}^{2017}+1}{2}$ |
5.设椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1的左焦点为F,右顶点为A,点P在椭圆上,若FP⊥PA,则直线PF的斜率可以是( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 1 | D. | $\sqrt{3}$ |
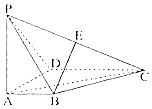 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=1,$AB=\frac{1}{2}$,点E为棱PC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=1,$AB=\frac{1}{2}$,点E为棱PC的中点.