题目内容

20．方程$|x|-2=\sqrt{4-{{（{y-2}）}^2}}$表示的曲线是（　　）
A．一个圆B．半圆C．两个圆D．两个半圆

分析 由题意，x≥2，方程化为（x-2）2+（y-2）2=4；x≤-2，方程化为（x+2）2+（y-2）2=4，即可得出方程$|x|-2=\sqrt{4-{{（{y-2}）}^2}}$表示的曲线．

解答 解：由题意，x≥2，方程化为（x-2）2+（y-2）2=4；x≤-2，方程化为（x+2）2+（y-2）2=4，
∴方程$|x|-2=\sqrt{4-{{（{y-2}）}^2}}$表示的曲线是两个半圆，
故选D．

点评 本题考查曲线与方程，考查分类讨论的数学思想，属于中档题．

练习册系列答案
相关题目
10．等比数列{an}中，a3+a5=10，a4+a6=20
（1）求{an}的通项公式；
（2）设${b_n}={（-1）^n}{log_2}{a_n}$，求数列{bn}的前29 项和S29．
11．已知点P（a，b）关于直线l的对称点为Q（3-b，3-a），则直线l的方程是（　　）
A．x+y-3=0B．x+y+b-a=0C．x+y-a-b=0D．x-y+3=0
8．已知函数f（x）=g（x）•h（x），其中函数g（x）=ex，h（x）=x2+ax+a．
（1）求函数g（x）在（1，g（1））处的切线方程；
（2）当0＜a＜2时，求函数f（x）在x∈[-2a，a]上的最大值；
（3）当a=0时，对于给定的正整数k，问函数F（x）=e•f（x）-2k（lnx+1）是否有零点？请说明理由．（参考数据e≈2.718，$\sqrt{e}$≈1.649，e$\sqrt{e}$≈4.482，ln2≈0.693）
15．直线m，n满足m?α，n?α，则n⊥m是n⊥α（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分又不必要条件
5．若圆x2+y2=1与圆x2+y2+6x-8y+m=0相切，则m的值为-11或9．
12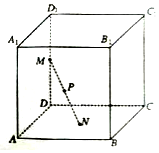．如图，已知正方体ABCD-A1B1C1D1的棱长为1，长为1的线段MN的一个端点M在棱DD1上运动，点N在正方形ABCD内运动，则MN中点P的轨迹的面积为（　　）
A．$\frac{π}{2}$B．$\frac{π}{16}$C．$\frac{π}{8}$D．$\frac{π}{4}$
9．已知x≥5，则f（x）=$\frac{{x}^{2}-4x+9}{x-4}$有（　　）
A．最大值8B．最小值10C．最大值12D．最小值14
19．对于任意两个向量$\overrightarrow{a}$，$\overrightarrow{b}$，下列说法正确的是（　　）
A．若$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$|＞|$\overrightarrow{b}$|，且$\overrightarrow{a}$与$\overrightarrow{b}$同向，则$\overrightarrow{a}$＞$\overrightarrow{b}$B．当实数λ=0时，λ$\overrightarrow{a}$=0
C．|$\overrightarrow{a}$•$\overrightarrow{b}$|≤|$\overrightarrow{a}$||$\overrightarrow{b}$|D．|$\overrightarrow{a}$-$\overrightarrow{b}$|≤|$\overrightarrow{a}$|-|$\overrightarrow{b}$|

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网