题目内容
根据下列条件,分别写出直线的方程:
(1)过点(3,2),斜率为2;
(2)过点(3,2),且与x轴垂直;
(3)经过点A(-3,4),与两坐标轴围成的三角形的面积为3.
(1)过点(3,2),斜率为2;
(2)过点(3,2),且与x轴垂直;
(3)经过点A(-3,4),与两坐标轴围成的三角形的面积为3.
考点:直线的一般式方程
专题:计算题,直线与圆
分析:(1)设所求直线方程为y=2x+b,代入(3,2)即可得到;
(2)由于直线与x轴垂直,则设直线为x=x1,由过点(3,2)即可得到;
(3)设所求直线方程为:
+
=1,由过点(-3,4)得到一方程,再由三角形的面积公式,得到一方程,联立解出它们即可.
(2)由于直线与x轴垂直,则设直线为x=x1,由过点(3,2)即可得到;
(3)设所求直线方程为:
| x |
| a |
| y |
| b |
解答:
解:(1)设所求直线方程为y=2x+b,代入(3,2)可得,b=-4,则直线方程为y=2x-4;
(2)由于直线与x轴垂直,则设直线为x=x1,由于过点(3,2),故直线方程为x=3;
(3)设所求直线方程为:
+
=1,
则代入点A(-3,4),则有
+
=1,①
又与两坐标轴围成的三角形的面积为3,
则
|ab|=3②
由①②解得,a=3,b=2或a=-
,b=-4,
则所求直线方程为:2x+3y-6=0或8x+3y+12=0.
(2)由于直线与x轴垂直,则设直线为x=x1,由于过点(3,2),故直线方程为x=3;
(3)设所求直线方程为:
| x |
| a |
| y |
| b |
则代入点A(-3,4),则有
| -3 |
| a |
| 4 |
| b |
又与两坐标轴围成的三角形的面积为3,
则
| 1 |
| 2 |
由①②解得,a=3,b=2或a=-
| 3 |
| 2 |
则所求直线方程为:2x+3y-6=0或8x+3y+12=0.
点评:本题考查直线方程的求法,考查待定系数法求方程的方法,考查运算能力,属于基础题.

练习册系列答案
相关题目
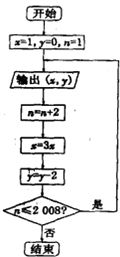 已知某算法的程序框图如图,若将输出的(x,y)值一次记为(x1,y1),(x2,y2),(x3,y3)…,(xn,yn)…若程序进行中输出的一个数对是(x,-8),则相应的x值为( )
已知某算法的程序框图如图,若将输出的(x,y)值一次记为(x1,y1),(x2,y2),(x3,y3)…,(xn,yn)…若程序进行中输出的一个数对是(x,-8),则相应的x值为( )